ニュートンの重力理論
相対性理論によるの重力理論に進む前に、ニュートン力学における重力理論のおさらいをしておきましょう。
二つの質点m1、m2間に働く力は、万有引力と呼ばれ
重力定数:G=6.7×10-11[N/m2/kg2]
となります。 有名なニュートンの万有引力の方程式です。
ここでm1、m2を地球と小さな質点とします。それぞれの質量をm、Meとしましょう。
式にすると、
です。 惑星のように、一方的に大質量の物体から質点が受ける引力を、一般的に重力と呼びます。
実際に地球周辺の重力場を計算してみましょう。
地球表面(半径): rs= 6.4×10-11[m]
地球質量: Me= 6.0×10-24[kg]
として計算結果をプロットします。
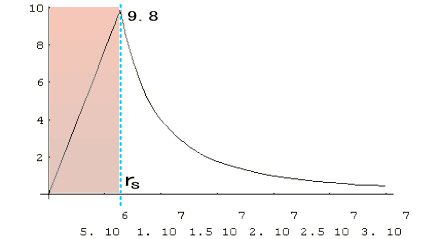
地球表面0.64万kmから、3万kmまでの引力の分布です。 地表では約9.8[N]から逆2乗に重力が減少していることが見て取れます。
尚、地球内部では質量密度を一定すると、中心からの距離に比例して重力が増加します。
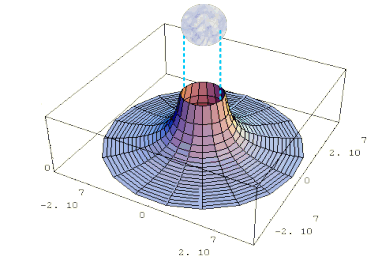
同様に、地球の周り(二次元)での分布です。
よく見かける図ですね。
次に重力場のポテンシャルを求めてみましょう。 重力に逆らってポテンシャルの低い所から、高い所に質点を移動させると、ポテンシャルエネルギーが増えます。
重力αは先ほどのニュートンの万有引力の方程式より
です。
また、ポテンシャルは、
です。
分布形状は以下の図の様に、質量に近づくほど落ち込んでいくいわゆる”じょうご型”です。
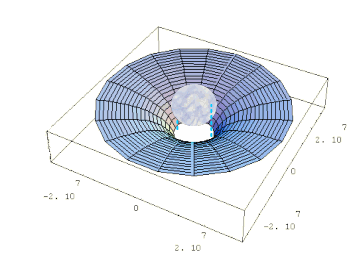
以上が、ニュートンの万有引力、つまり力:Fが主役で、ポテンシャルがおまけの脇役とした重力の表現方法です。
次に重力場方程式を、質点が一個の場合の単純なものから、質量が散在する状況を記述できるように一般化してみましょう。
 Dr.メイの『重力場理解のための、イメージトレーニング』!  質量からは仮想の重力線注)が湧き出している。  質量が大きいほど、線の数が多い。 質量は重力線を供給する源泉と考える。 注)重力線という物理実態は存在しない。 重力場を考える上で、電磁気学における電気力線と同じように、思考を助けるための便宜的な力線。 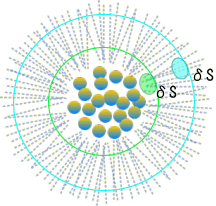 ある空間点で、単位面積δSあたりの重力線が多いほど、重力は強い。 [重力=重力線密度] 質量を囲った緑の球面も青の球面も、突き抜ける重力線の総数は同じ。結果、緑の重力線密度が青より高くなる。 だから、質量源に近い方(緑)が重力は強くなる。 半径Rの球の面積は4πr^2。 重力線密度は1/4πr^2に比例。 だから重力は逆二乗の力となる。 重力は重力ポテンシャルφを創る。重力(加速度)を積分すると重力ポテンシャルとなる。 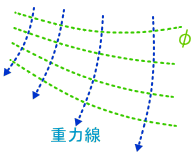 ポテンシャルはスカラー。 複雑な質量分布でも、距離だけでポテンシャルを計算し、空間軸で微分すると重力加速度のベクトルを求められる。 等ポテンシャル面に垂直に、重力線が走る。 等ポテンシャル面の間隔が詰んでいるほど、重力線の密度も高くなる。 |
ポアッソンの方程式
今後、テンソルの方程式として扱うための準備として、重力も重力加速度としてベクトル化します。
ベクトルrを重力源を原点とする位置ベクトルとします。 重力加速度αは原点向きに向かうベクトルであるため、位置ベクトルを基準に取ると、負の符号が付きます。
ポテンシャルφはスカラーです。 重力加速度の積分なので、符号が反転し、正のスカラー場となります。
複数の質点Mが距離rを隔てて存在する場合
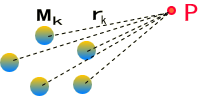
点Pにおけるポテンシャルφは重ね合わせられて
で与えることが出来ます。
以下の様に任意の曲面Sで囲まれた領域中に、質点が複数存在し、その全質量がMである場合、
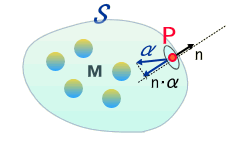
その曲面上での重力加速度の法線成分α(つまり面の外に垂直な単位ベクトルnとの内積)を、Sの全曲面にわたって積分すると
と表されます。 これは重力場でも、電荷による電場(電界)でも同じであり、電磁気学ではガウスの定理と呼ばれる基本的な法則です。
∇はスカラー場に対しては、傾斜を表す演算子で、ナブラと呼ばれます。
gradφとも書き、演算結果は傾きの方向を表すベクトル場を与えます。
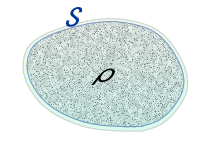
この考えをさらに推し進めて、質量密度ρである領域に適用すると、
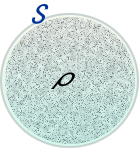
例として、地球のように球形の質量密度分布(一定と仮定)における、重力ポテンシャルφと重力加速度αの分布です。
さらにガウスの定理は
と拡張できます。
重力ポテンシャルの傾斜:gradφ(=∇φつまり重力)を取り、さらにその発散(div gradφ)は
となります。 この演算は2回の偏微分なので∇2と表現し、ナブラの2乗と呼んだり、
の様にラプラシアン:⊿という演算子で表現したりします。
重力の発散とは『重力線の湧き出し口』が増えることを意味し、質量の分布しない空間(ρ=0)からは重力線が増えない事を意味します。
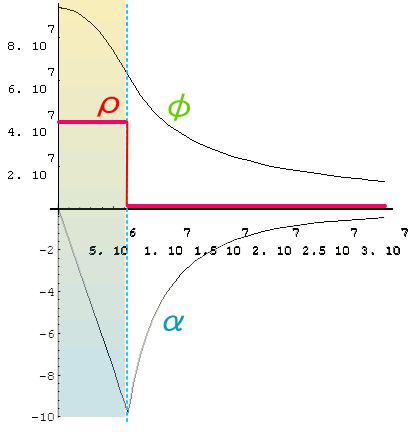
この地球の例では質量密度が均一に分布していと仮定しているため、重力加速度の大きさ|α|は、地表まで直線的に増えるわけです。
地表を過ぎると質量密度はゼロになります。 重力線の湧き出し口が無くなるため、これ以上領域Sを広げてても、領域S上の重力線総数は増えません。 逆に閉領域V内の質量密度とS面上の重力線密度は同時に下がっていきます。 その事が|α|の減少に現われていると見ることが出来ます。
この式はポアッソンの方程式と呼ばれ、電磁気学等でもよく利用されます。
このポアッソンの方程式
により重力場を記述すると、万有引力Fが表に出てきません。
相対性理論の基本は物理量を4元化し、テンソル方程式により物理法則を記述することにあります。そういう意味では単純な引力Fは相対性理論における重力理論の出発点にはなり得ません。
今まで見てきたように、時空の曲がりと重力場との間には、密接な関係予想されます。このポアッソンの方程式の左辺は、∇iφという4元ベクトルに拡張可能な量を含んでいます。
以降、この方程式を相対性理論化する、つまりテンソル方程式に拡張することを考えましょう。
==続く==