| アインシュタイン・テンソル よし、手始めにコンピュータ実験での手順を、もう一度数式を使って整理してみよう。 ビアンキ恒等式 ↓縮約 ↓縮約 という手順だった。 と言う事は、 と言う事だ。 ところで、gの共変微分は通常の微分 での定数C並だ。 つまり、関数の積のの微分のような、めんどくさい微分をする必要なく、 と書ける。 左辺第1項の_部分に注目し、ビアンキの関係式 を使い変形すると となる。 よって、恒等式は となる。 第3項にh,iの反対称性を適用し、 第2項、第3項のhを縮約すると 後はgの添字を縮約し、 となる。 ここで、第2項のダミー添字jを第1項のhに統一し1項、2項を足し合わせ 得ることが出来る。 さらにgklを両辺に掛けて、 ↓ ↓ と、微分用のダミーインデックスをhに統一できる。 共変微分の添字をカッコの外にくくりだし、両辺に1/2を乗ずれば となる。 そう、このカッコの中が非常に重要だ。 ビアンキの関係式を適用しながら、ビアンキの恒等式を縮約た結果の、全エキスがこの中に詰まっているはずだからだ。 お! いかん、いかん。 ずうっと、添字にローマ字を使い続けていた。 ギリシャ文字に戻そう。 カッコの中のテンソル式様にお名前をお付けししなければ。 そうだな、テンソル名は神々しいから、Gにしよう。 犬言訳者注:以下、意味不明の神がかりな文章が続く。可能な限り犬言に忠実に翻訳を試みたが、物理学として数式以外は参考にしないことをお奨めする。 どうだ、これが神々しき、宇宙の真理テンソル様のお姿だ! そして、その為せる技は、共変微分した式 で在らせられる。 宇宙の真理テンソル様の為せる技は、天上界ではビアンキの恒等式と呼ばれ、そして我々の地上界に降臨されし時には、この様な技を為されるのである。  へ? 何々、 ちゃんと最後まで教科書読んだのかだって? ええっ! なに、何とこれが『アインシュタインのテンソル』のことだって?!・・・ ・・・ふん! 人に、じゃなくて、犬に散々めんどくさい実験やら、解説させといて、黙って見ていたくせに。 ぷんぷん! もう実験なんかやってやらない! ・・・ え? 3時のお茶に、取って置きのドーナッツを用意してくれるって? だから機嫌を直して、実験を進めてくれだって・・・。 ほ、ほんとかい? も、勿論! すぐ機嫌なんて取り戻せるぞ! ほら! このシッポを見てみろ。  ほら! ほら! さあ、次の実験何だっけ? 何、何、 RμνとRについての挙動確認? お安い御用! リッチ・テンソル Rμνはリッチ・テンソル(Ricci tensor)と呼ばれている・・・と、教科書に書いてあった・・・。 早速、R4を縮約しよう。 対称性の無い添字どうしのhとkに付いてだ。
ほい! 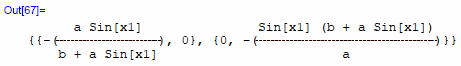 ふむ。対称性が有りそうだな。
いつもの様に、対称性の確認。 OK! 大サービスで添字を入れ替えるテクニック。 Transpose[変数,{入れ替え位置指定}]
と簡単に確認できる. ビアンキの恒等式の巡回置換で使えたかな? スカラー曲率 Rはスカラー曲率と呼ばれている。 やはりIgxxにより、縮約。
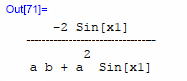 ふむ。 これはちょっと興味があるな。 トーラスのガウス曲率は場所によって+/-した。 リングの内側側面が(-)で、外側側面が+。 そして天と地の部分が曲率0だった。 このスカラー曲率Rはどのような分布なのかな? グラフに書いてみよう。 x1がパイプの径方向の座標軸だ。 天が0 、外の赤道がπ/2、地がπ、内の赤道が3π/2 となるように座標を取ってある。
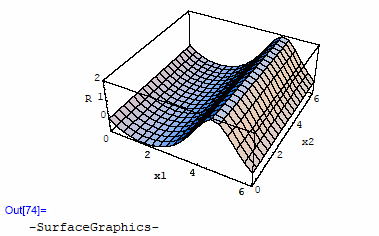 なるほど、ガウス曲率Kとは符号が逆だな。内側(3π/2付近)が狭くなっているから曲率は大きい。 x2方向には曲率の変化は無い。 さあ、私が発見したと思っていた宇宙の真理テンソル様。じつはアインシュタインテンソルだったが。 これが、共変微分で0となるのを、直接確認してみよう。 Gは2階のテンソルなので、テンソルの共変微分のルールを適用して
 ・・・。 そういえば、球面での実験は途中でやめちゃったんだっけ。 よし、大サービスで球面のリッチテンソルとスカラー曲率Rも計算しておこう。 リッチ・テンソルはOut[126]。 そして・・・はらほら、Out[129]にある通り、Rは全然変化しない。グラフでもまっ平ら。 これが『球面はつまらない空間だ』の原因だったのかな。 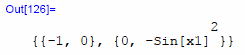 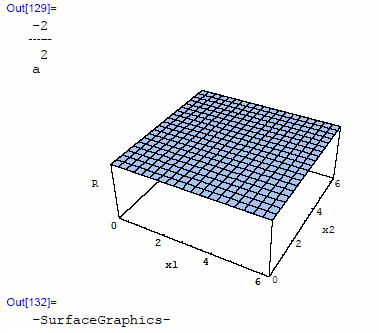 ちなみに、球面のガウス曲率K(=1/a2と)は逆符号で2倍、 G=-2K となっているな。 さあ、終わったぞ。 早くお茶にしょう。 ほれ。ほれ!  さあ、ドーナッツ! 早く。 早く。 ほれ。ほれ!  |
あれ? アインシュタイン・テンソルがゼロであることを、メイは気にかけようとしないですね。 きっとドーナッツのことで、頭の中が一杯なんでしょう。
しょうがないので、お茶にでもしますか。