曲率テンソルを利用して重力場の理論を構築するための、数学的な準備をもう少し進めておきましょう。
ベクトルの積を微分する場合、次の様に『関数の積の微分』が成り立ちます。
同様にベクトルの共偏微分も『関数の積の微分』が成り立ちます。
以降、共変微分オペレータを右に ”▽μ” と書く変わりに ”:μ” と変数の右に書くようにします。つまり上記の式は
以下、式の変形の大筋を参照文献・図書 (1) の第13節を参考に、独自の説明を補足
のようになります。ちなみに、ただの偏微分は”,μ”とカンマで書くようにします。
すっきり見やすく、また記述もしやすくなりました。
これを展開します。
μとνを入れ替えて引く、つまり曲率テンソルを求める操作により
この中で、ベクトルの積をテンソルと見なすと
さらに、このテンソルの成分
が導出できます。
この式の右辺はインデックスβ,μ,νの順序に依存しない項から成っています。そこで、等式の左辺も含め、以下の様に循環的に入れ替えて見ると
を得ます。これを基(表の②巡回置換1回の項)にして、さらに巡回置換2回分の方程式を生成します。
| 左辺 | 右辺 | ||
| ① | 巡回置換0(=3)回 | ||
| ② | 巡回置換1回 | ||
| ③ | 巡回置換2回 | ||
| ④ | 巡回置換3回 |
②から④の三つの式の両辺を足し合わせます。 そうすると、この内、右辺のアンダーライン ”_” を引いた項は、恒等式の
さらに、2重アンダーライン ”=”を引いた左右の項同士、打ち消しあって消えてしまいます。
結局、式の中で残ったものは
だけとなります。 任意のベクトルVで成り立つための条件として
参照文献・図書 (1) の参考範囲終了
という恒等式を得ることが出来ました。この式はBianchiの恒等式(ビアンキの恒等式)と呼ばれ、重力場の理論を構築する上で、非常に重要な恒等式となります。
尚、曲率テンソルRの非独立な関係式(種々の対称性や前出の微分しない方の恒等式)と合わせて、これらをビアンキの関係式と呼びます。
 うーん。 ここなあたりが実感できる、ちょうど良い物理実験を、なかなか思いつけない。 うーん。 ここなあたりが実感できる、ちょうど良い物理実験を、なかなか思いつけない。しょうがないから宇宙船のコンピュータを使ってみよう。 そう、あの「快適モード』で私をひやひやさせた、気の利かない、頑固なおんぼろコンピュータだ。 数式処理を使えば、ちょとした実験気分が味わえる。 ちょうど、数式処理言語としてポピュラーなマセマティカ(Mathematica)が有ったはずだ。 MathematicaはWolfram Research, Inc.の登録商標です。 今までの復習を兼ねて、これを使って確認をしてみよう。 尚、理解を深めるため、Mathematicaの実行はコンピュータと会話形式により1ステップづつ実行しよう 。 物理を勉強する上でMathematicaなどの数式処理言語は便利だ。ちょうど数式処理入門講座にもなるかな? さて、コンピュータ君。 Mathematicaをロードしてくれたまえ。 ↓全Mathematicaソースをご利用いただけます  おう、よしよし。 ちゃんと起動できたみたいだ。 まずは初期設定。 Off~の行はスペルエラーの表示を止めるコマンド。 通常はオフしない方が良いかも。
座標系の変数はxとし、その要素を{x1,x2,x3,x4}と指定しておく。 現実世界は四次元時空だから最大x1~x4まで四個の座標軸が必要だ。 それ、実行。  よし、よし。 Out[4]に結果が出力された。うまく設定できたようだ。 私が行ってきた実験は球面上などの二次元物理空間であった。そこで当面、計算は二次元で行うことにする。 変数Mに次元数2をに設定し、最初のに行った球面上の実験を再現させてみよう。
変数gaは球の半径。ParametricPlot3Dにより半径1の球面図の生成ができる。 最後の行のgxx、これが一番重要だが、この球面に対応する計量を、対角行列関数(DiagonalMatrix)により設定する。 半径a球面のメトリックスは 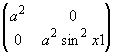 であるが、対角成分のみの指定でOK。 以上を一挙に実行しよう。 ちょっと年代物のコンピュータ君だから、ちゃんと動くか心配だ。 それ実行!  ・・・ さて、どうかな? 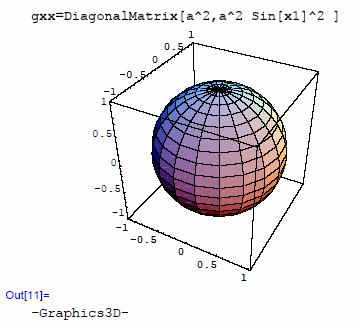 おお!なんと懐かしい、2次元球面! 続いての出力は、計量の設定報告か。 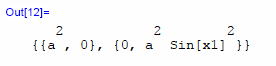 この数式処理では、行列をリストとして扱い、その要素を{ }で囲って表現する。 このOut[12]のリストは 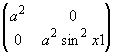 という行列が設定されたことを表現している。 テンソルの成分は、このように行列の要素として扱い、計算すればよいことになる。 尚、添字位置が左寄りなほど、カッコのネストは大ぐくりとなる。 Igxxに計量gxxの逆行列を生成しておこう。
と入力して、それ! 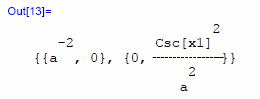 おう、快適快適。 逆行列の計算結果が即座にOut[13]として表示された。 よし、これで、あらかた準備完了。 早速、リーマン接続であるクリストッフェルの三指標記号2種類 第1種クリストッフェル記号: 第2種クリストッフェル記号: を求めてみよう。この数式処理では、ギリシャ文字を変数として使えないので、数式の方もローマ字を使うことにする。 尚、今までの式とはgの添字位置が、左右異なっている個所があるかもしれない。だが、gは対称テンソルだから、気にする必要は無い。 対応するコマンドを、入力しながら解説してみよう。
まず最初のTable関数は、行列の各要素を、計算しながら生成するコマンドだ。 Table[ 要素の計算式, {i,2},{j,2},{k,2} ] のようにして使用する。 この場合は変数Chrに i,j,k を添字とする量が生成されたことになる。 計算式の中身は、クリストッフェル記号の式そのままだ。 D[式, {変数}] により偏微分を行う。 また、縮約は Sum[項1[i]*項2[i] , {i,2}] Sum関数により積和をとる。 計算結果はTable関数に渡され、リストの要素にセットされる。 Out[15]が計算結果だ。これが第1種クリストッフェル記号の要素をリスト表示したものだ。 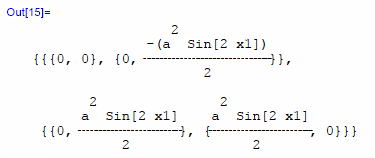 第2種クリストッフェル記号は最初の添字を上げたものだ。第1種クリストッフェル記号に計量gxxの逆行列Igxxをかけて作る。
 確か、添字のどれかに対称性が有ったはずだ。ついでに確認しておこう。 とりあえず[i、j]を入れ替えて引き算してみよう。
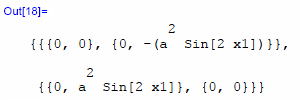 ん、ゼロにならない。 外れだ。 じゃあ[j、k]だ。 それ。
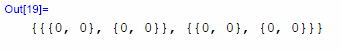 お! ゼロになった。 第2種の方も同じかな?
 たしかに教科書に載っていた対称性だ。  リーマン接続の対称性 ふーん、なるほど。 年代物のポンコツだと思っていたが、君、結構役に立つじゃないか。 次にリーマン・クリストッフェルの曲率テンソルを計算させよう。数式は、 だ。 接続記号の下付き添字も、前回の数式での表示とは順番と変わってしまっているかもしれない。だが、先ほど確認した対称性が有るので問題は無い。読み合わせで不便かもしれないが、あしからず。 まず分りやすく の部分を計算。 D[式,{変数}]により偏微分を行う。 結果をDChrに設定しよう。
 次に残りの の計算だ。Sumは添字[l ]に関する縮約。 結果はCChrに取っておく。
 二乗の項が増えて、ごちゃごちゃとした結果だ。 おう、そうそう。 この項が私に曲率の実験の時「ベクトルをぐるっと回せ」とか何とか囁いていたのだっけ。 よし、いよいよ曲率Rを求めるぞ。 添字の数が4つだから、変数名をR4としよう。 行列の加算演算はそのまま二つの項を足し合わせばよい。
 簡単簡単。じつにらくチン。 ふーむ。 これがリマ-ン・クリストッフェルの曲率テンソルなのか。対称的で意外にすっきりしている。 そうそう、R4のベクトルで対称性を探ってみようと思っていたんだ。 その後教科書にも色々出てたが、実感がわかない。それにちょっと眠くもなったりしたもんだから。 丁度良い機会だ。 この際、直接確認してみよう。 まずは添字[h]を下げ、全部共変成分に揃えてみよう。 より対称性が、あらわになりそうな気がする。 数式で書くと
 フムフム。 添字を下げると、こうなるのか。 R4の成分とは微妙に違っている。 同じ形の項が並んだぞ。 //MatorixFormを使ってもすこし見やすくしてみよう。 尚、点線の枠は、私が見やすくするために書き込んだものだ。  よしよし、見通しが良くなった。 ちょっと隙間が多いのが寂しいかな。きっと対角成分のみの計量を使ったからなのだろうけど。 物によっては実証とまではいかないだろうが、教科書での式の意味を理解するのには役に立ちそうだ。 早速確認に入ろう! まずは反対称性 私がジープに乗ってベクトルの平行移動を実験していたとき、移動ルートが逆順の場合を考えたら、すぐに見つかった対称性だ。 [Jk]をひっくり返して・・・、 それ!
 ・・・オールゼロ。 よし! これはルートの逆周りで、ベクトルの回転も逆に回るという事の再確認だ。 cR4[[h,i,k,j]]の出力を%//MatrixFormにより出してみた。%は直前の出力を記憶している。 要素がどのように反転しているのか、確認してほしい。  次は
それ! ・・・どうかな?  おお! やはり期待した通りだ。 当然cR4[[i,h,j,k]]を表示させると同じもの。何せ等式だから。  次に[h,i] と[j,k]のそっくり入れ替えた
 これは正の対称性だ。 もちろんcR4[[j,k,i,h]]はcR4[[i,h,j,k]]と同じフォームをしている。  そうだ。 重要な関係式が有ったな。 これだこれ。 曲率のクリストッフェル記号を眺めていたら発見できたやつだ。ビアンキの恒等式を導き出すときに使った片割れのような恒等式だ。 早速、確認。
それ!  当然の結果。 よし! ところで、 の方はどうかな?
 やはり同じだ。 曲率テンソルは実に対称性が豊富で美しい!?・・・うーん。別の言い方をすると、ちょっと無駄が多いとも言えるのかな? 単純な対称性だけでも、あらためて書き出すと、 そういえば、教科書に書いてあったな。 えーっと、『四次元時空での曲率成分は4の4乗で256だが、対称性により独立な成分は、たったの20個でしか無い』とか、なんとか。 あと、残っている対称性は だったかな。 それとビアンキの恒等式の片割れの恒等式 なのだが、上に列挙した対称性により、左辺の添字がどれか同じ場合、恒等式以前に左辺自身が0になっしまう。 例えば、11**とか、121*とか、・・・?? あれ? 二次元だと全部そうなっちゃうのかな? 四次元の場合は1234の巡回だけが生き残っていたはずだが。三次元以下では、そもそも次元数が足りない。 全滅だ。 この片割恒等式君は四次元以上ではじめて意味をもつ恒等式みたいだ。 まあ、以上がリーマン・クリストッフェルの曲率テンソルとその対称性に関する整理といった所かな。 さて、いよいよ実験の主題、ビアンキの恒等式の確認に入ろう。 もう一度書くと、ビアンキの恒等式は であった。 この式は曲率テンソルを3個、アンダーラインを引いた添字を巡回させながら共変微分するように構成されている。 ところでRは上下に添字が出てくる混合テンソルだ。 テンソルの共変微分は以下のルールの通り。 上下の添字の数に制限は無い。 テンソルの全添字を一つずつ接続係数Γと縮約する ・接続Γと縮約する添字が反変成分なら+ ・接続Γと縮約する添字が共変成分なら- ちなみにベクトルの共変微分の場合は、偏微分項と第一番目の縮約項のみの見慣れた形の式となる。 さてこのルールを曲率テンソルに適用する。TをRに換え、変数はbi1[h,i,j,k,l]とし、(i,j,k)を巡回させて、残りの二つの項bi2、bi3を生成する。 まずは、第1項。 縮約はお決まりのSum関数だ。
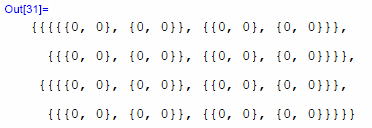 ふむ。全てゼロ。 次に第2項。
 ・・・ゼロ。 次、第3項 ・・・。 巡回元が全てゼロなので、空しいけど、とりあえず実行。
 ふん。 コンピュータ君はちゃんと動いているみたいだな。 ばかばかしいけど、最後に等式の確認。
 んー。 実につまらなかった! 球面とは、実はつまらない空間だったのかな? 確かに、非常に対称性の高い単純な形状だと言えば、そうなんだが。 よし、ちょっと複雑な二次元曲面に替えてみよう。 ドーナッツ型二次元曲面はどうかな? いわゆるトーラスというやつだ。 こいつは見るからに複雑そうだぞ。 場所によってガウス曲率Kも+/-しているみたいだし。 そうと決まったら早速生成だ。 パイプをグルッとリングにして、つなげた形になる。 パイプの半径をa、リングの半径をbとすると、グラフィックの生成式は以下の通り。基本的には球面と同様にParametoricPlot3D関数で生成できる。a,bの形状を決める定数をga,gbとし今回はパイプ半径1、リング半径2としてみよう。 この表面の二次元曲面空間における計量は 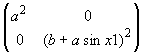 となる。 これを、計量変数gxxに設定し、合わせて計量の逆行列Igxxも計算しておこう。
さあ、どうかな。 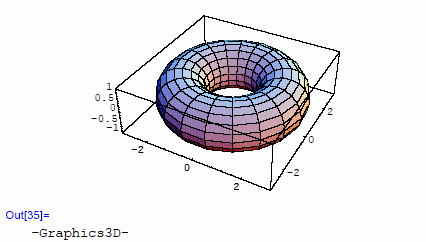 お、見事なドーナッツだ。 おいしそう! 思わず、よだれが出てくる。 早く実験を終わりにして、お茶とドーナッツにでもしたいもんだ。 よし、先を急ごう。 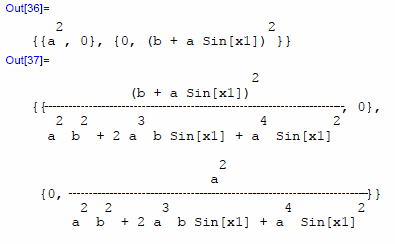 次の出力は、計量とその逆行列の設定結果だ。 あさ、ドーナッツ空間の準備が出来た。 球面と同じ手順で確認して行こう。 まずは、リーマン接続。第1種、第2種のクリストッフェル記号を一気に計算。
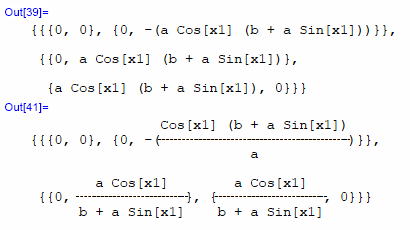 やはり、球面より複雑になるのは仕方が無いかな。 但し、見ての通り対称性は球面と同様に確認できる。 さて、次なるは曲率テンソル。 球面と全く同じ式を再入力。
お気づきだと思うが、トーラスに替えたことによって変わった部分は、計量テンソルの成分式のみだ。 つまり、リーマン幾何学では計量の上に構築されている。 ここなあたりが計量が基本テンソルと言われる所以であろう。 さあ、実行。 ・・・少々、時間がかかってるかな?  よしよし。 多少ごちゃごちゃしているが、最後のOut[45]がR4、つまり曲率テンソルの成分式だ。 合わせて添字を下げておこう。 cR4に設定だ。これも球面と同様の手順だ。
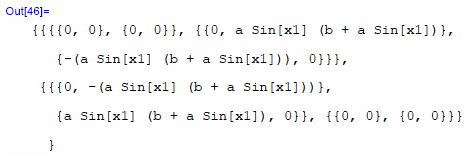 ビアンキの恒等式の片割の確認。
 OK! と言っても先ほどの実験で考察した通り、二次元空間では虚しいのだがが。 さて、いよいよだ。 先ほどの球面より複雑なトーラスだぞ! まずは第1項から。 また、いきなり全成分ゼロだなんて、いやだからな!
それ、どうだ・・・。    おお、出た!出た。 すごいじゃないか。今度はちゃんとゼロじゃない成分だ。 おお、出た!出た。 すごいじゃないか。今度はちゃんとゼロじゃない成分だ。ポンコツ君・・・、じゃなかったコンピュータ君ご苦労、ご苦労。 よしよし、この調子で続きの2つを一気に計算だ。
 ウーン、全体的に複雑。 ビアンキの恒等式がはたして成り立つものかちょっと不安になる。 が。まあ、心配しても始まらない。
それ、実行! 今度はゼロになれ、ゼロ!・・・ 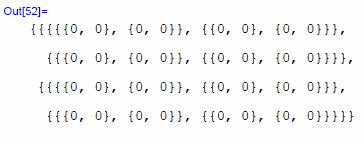 おお! やったやった。 見事にゼロだ! OK! ビアンキの恒等式はちゃんと成り立っている。 形が複雑になるとビアンキの恒等式の意味が出てくるようだ。 一応、これで満足、満足。 実験を続ける意味が出てきたわけだ。 それでは今しばらく、元の球面から離れて続きを始めよう。 次にやることだが、このビアンキの恒等式を縮約してみよう。 R4は対称性が豊富で、まだまだエキスにまで到達してないような感じだ。物理を記述するためには、もっと無駄を絞って単純化できるのではという気分になる。 このビアンキの恒等式において、対称性の無い添字どうしを縮約してみよう。まずは[h]と[l ]あたりから。 ↓ まずはビアンキの恒等式と同様手順で、3つの各項を縮約。
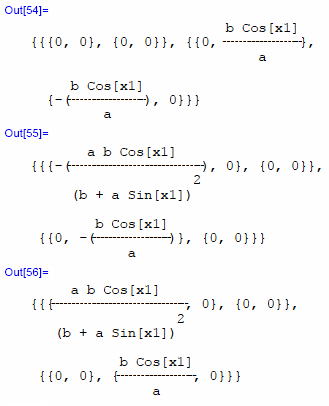 ちゃんと成分は有る。 さて縮約恒等式の値、つまり各項の合計であるcntBIはどうなった調べてみよう。 それ!
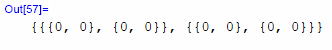 やはり、最後の合計値は全てゼロだ。 元のビアンキ恒等式と傾向は同じだな。 ええい! ここまで来たらこの傾向の続く限り地の果てまでも縮約だ!
どうだ!
まいったか☆!★?。 ・・・ 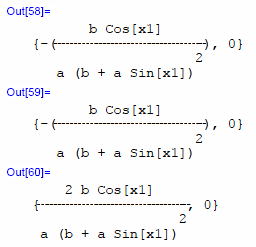 ・・・  ウワァァァ! 何と、まだ同じ傾向。 げ・に・恐・ろ・し・き、ビアンキの恒等式! ウワァァァ! 何と、まだ同じ傾向。 げ・に・恐・ろ・し・き、ビアンキの恒等式!恒等式のエキスは、最後の最後、添字1個まで縮約しても、まだ残っている。 いや、これはきっと宇宙開闢以来の由緒正しき方程式様に違いない。是非、そのお姿を拝見させてもらいたいものだ。 |