丂嬻娫偵暘晍偡傞儀僋僩儖摍偺暔棟検傪丄曃旝暘偡傞偙偲傪峫偊傑偡丅丂嬻娫偑暯傜側応崌丄
丂丂
偲側傝丄寢壥偼旝暘偡傞弴斣偵娭學桳傝傑偣傫丅
偲偙傠偑丄嬻娫偑嬋偑偭偰偄傞応崌偺嫟曄旝暘偱偼丄
丂丂
偑乭0乭偵側傞偲偼尷傜側偔側偭偰偟傑偄傑偡丅丂偮傑傝旝暘偡傞弴斣偱丄寢壥偑曄傢傞偲尵偆偙偲偱偡丅丂偙偺帠傪悢妛偱偼丄嫟曄旝暘偼亀壜姺偱偼側偄亁偲尵偄傑偡丅
偦偺弴斣偵傛傝曄傢傞検傪埲壓偺條偵儕乕儅儞嬋棪丗R偱昞偟傑偡丅
丂丂
偙偺嬋棪偼惓妋偵尵偆偲丄Riemann乚Christoffel偺嬋棪僥儞僜儖偲尵偄傑偡丅偦偟偰偙偺嬋棪偼嫟曄旝暘偺惗偄棫偪偱暘傞傛偆偵丄嬻娫傪峔惉偡傞寁検乮儊僩儕僢僋僥儞僜儖乯偐傜摫偒弌偝傟偰偄傑偡丅
丂丂丂寁検丗丂丂丂丂丂丂丂丂
丂 丂丂伀
丂丂丂儕乕儅儞愙懕丗丂丂丂
丂 丂丂伀
丂丂丂嫟曄旝暘丗丂丂丂丂丂
丂 丂丂伀
丂 丂丂嬋棪僥儞僜儖丗丂丂
偐側傝丄怓乆側忣曬偑媗傑偭偰偦偆側僥儞僜儖偱偡丅丂儊僀偑峴偒媗傑偭偰偟傑偭偨亀嬻娫撪偺摴嬶棫偰偺傒偱丄偦偺嬻娫偺嬋偑傝嬶崌傪掕媊偡傞亁偲偄偭偨偙偲偑丄弌棃傞偐傕偟傟傑偣傫丅
偦偺曈偺帠忣傪妋擣偡傞偨傔丄儕乕儅儞嬋棪偺摫弌夁掱傪傕偆彮偟惍棟偟偰傒傑偟傚偆丅
僀儞僨僢僋僗傗僟儈乕僀儞僨僢僋僗偺憡屳娭學偵拲堄偟側偑傜丄擇抜奒偵暘偗偰旝暘偟傑偡丅
傑偢惓弴偱偡丅
丂丂
丂丂丂丂丂丂丂丂
摨條偵丄媡弴偺旝暘傪偟傑偡丅
丂丂
惓弴偐傜媡弴傪堷偒傑偡丅
丂丂
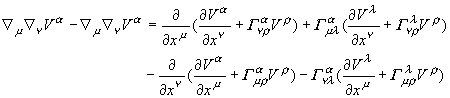
偝傜偵揥奐偟傑偡丅
丂丂
丂丂丂
偙偺拞偱丄
丂丂
偺崁偼兪丄兯偵懳徧側崁側偺偱徚偊偰偟傑偄傑偡丅丂傛偭偰丄
丂丂
丂丂
偲側傝傑偡丅
偙偺傛偆偵愙懕偩偗乮偩傜偗丠乯偺崁偑巆傝傑偟偨丅
尦偺掕媊偺
丂丂
偮傑傝丄儕乕儅儞嬋棪僥儞僜儖偼愙懕傪巊偭偰丄怴偨偵掕媊偡傞偙偲偑弌棃傑偟偨丅
丂偲偙傠偱丄愙懕偲偼丄儀僋僩儖偺暯峴堏摦帪偺嫇摦傪掕媊偡傞儅僩儕僢僋僗偱偡丅
偙偺拞偱丄
丂丂
偺崁傪丄偠偭偔傝偲挱傔偰偄傞偲丄亀儀僋僩儖傪暯峴堏摦偟偰暯峴堏摦丅丂傂偭偔傝曉偭偰丄暯峴堏摦偟偰暯峵堏摦亁偲偝偝傗偄偰偄傞傛偆偵暦偙偊傑偣傫偐丠
 壗丠嬋棪偑亀侐侓儀僋僩儖傪暯峴堏摦偟偰暯峴堏摦丂侒侓丂傂偭偔傝曉偭偰丄暯峴堏摦偟偰暯峵堏摦侓侓亁偲殤偄偰偄傞偭偰丠 壗丠嬋棪偑亀侐侓儀僋僩儖傪暯峴堏摦偟偰暯峴堏摦丂侒侓丂傂偭偔傝曉偭偰丄暯峴堏摦偟偰暯峵堏摦侓侓亁偲殤偄偰偄傞偭偰丠丂丂丂 偆乕傫丅丂偦偺傛偆側婥偑偡傞傛偆側丄偟側偄傛偆側丒丒丒丅偙偺崁偼堦晹偱偟偐側偄偐傜壗偲傕尵偊側偄傫偩偑丅 兪偲兯偼嬻娫堏摦倓倶傪庴偗帩偮僀儞僨僢僋僗偩偭偨丅丂偙偄偮傜偑撈棫偵慻傒崌傢偝偭偰偄傞偐傜丄偄傠偄傠側宱楬偱丄偖傞偭偲夞偭偰栠偭偰偔傞偲傕庢傟偦偆偩丅丂揰慄偺栴報偼儅僀僫僗偺崁偩偐傜丅 亀僌儖僢偲夞偭偰寢壥偼乭侽乭偠傖側偄偧両亁偲偱傕尵偄偨偺偐側丠 丂丂丂丂丂
暿偺尒曽偱亀 丂僌儖僢偲夞傞丠丂儚儞両丂偠傖側偐偨丅丂偊乕偭偲丄偝偭偒偺幚尡偱偼僌儖僢偲夞偭偰丄墌廃棪傪應偭偨傫偩丅丂崱搙偼儀僋僩儖傪僌儖僢偲暯峴堏摦偝偣偰丄曄壔傪應傟偲尵偭偰偄傞偺偐側丠 丂偦偆偐丄傗偭偰傒傞壙抣偼桳傝偦偆偩丅丂憗懍丄媴柺嬻娫偵峴偭偰丄幚尡奐巒両 傑偢丄僕乕僾偵儀僋僩儖傪搵嵹偡傞丅丂偳偆傗偭偰儀僋僩儖傪偔偭晅偗傞偺偐偭偰丠 娙扨娙扨丅戝偒側斅傪栴報偺宍偵壛岺偟丄偮偄偱偵栚棫偮傛偆僆儗儞僕怓偱揾偭偨偩偗丅屻偼丄庤摦偱偖傞偖傞偲曽岦妏搙傪曄偊傜傟傞傛偆偵丄夞揮幉傪庢傝晅偗偰弌棃忋偑傝丅 丂丂丂丂丂  偙傟偱丄幚尡弨旛姰椆丅屻偼僌儖僢偲夞偭偰傒傞偩偗偩丅墌廃忋傪夞偭偰傒偨偄偺偩偑丄愨偊偢嵟弶偺岦偒傪曐偮偨傔偺丄僕儍僀儘晅偒偺崅媺儀僋僩儖偑昁梫偵側傞丅丂 偦偙偱丄崱夞偼僌儖僢偲夞傞嵟掅尷偺儖乕僩偲偟偰丄嶰妏僐乕僗偵偟傛偆丅 丂傑偢丄奐巒揰嘆偼堒搙90亱偺愒摴偱宱搙侽亱偺揰丅丂偙偙偐傜儀僋僩儖傪僕乕僾偺恑峴曽岦偵僙僢僩偟堏摦奐巒丅 丂丂丂丂丂 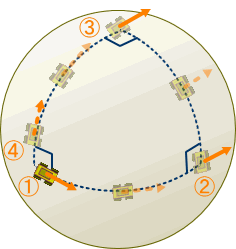 愒摴忋傪搶偵俋侽亱堏摦偟嘇偵摓拝丅丂媴柺偺侾/係傪墶抐偟偨偙偲偵側傞丅丂偙偙偱丄僕乕僾偺岦偒傪嵍偵俋侽亱丄偮傑傝杒嬌揰偵岦偗傞丅丂岦偒傪曄偊傞偺偼僕乕僾偩偗偱丄儀僋僩儖斅偼岦偒偑曄傢傜側偄條偵拲堄偡傞丅 偙偺傑傑堏摦偟丄杒嬌揰嘊偵摓拝丅傗偼傝俋侽亱嵍偵僕乕僾偺岦偒偩偗曄偊傞丅丂偙偺忬懺偱丄儀僋僩儖偼恀屻傠傪岦偄偰偄傞丅 屻偼丄恀偭捈偖撿壓偟愒摴忋偺奐巒揰嘆傪栚巜偡丅丂傕偆偡偖摓拝偩丅丂怳傝曉偭偰巚偄婲偙偡偲丄堏摦偼恀偭捈偖偱丄僴儞僪儖偼慡偔愗偭偰偄側偄丅丂偙偺僐乕僗偼應抧慄偲偄偆偙偲偩丅 偝偁丄摓拝両丂崱偺儀僋僩儖斅偺忬懺偼丄嘋偩丅丂憗懍丄嘆偲嘋偺曄壔検傪寁應丅丂偍偍両壗偲丄俋侽亱偢傟偰偟傑偭偰偄傞丅丂 偙偺丂 嬋柺撪偺摴嬶棫偰偺傒偱嬋偑傝嬶崌傪抦傞曽朄偑丄墌廃棪埲奜偵傕桳傝偦偆偩偲偄偆帠偩丅 丂偦偆偲暘偭偨傜偙偺嬋棪偺幃傪丄揙掙揑偵暘愅偟偰傒傛偆丅 擇師尦嬋柺傪峫傞丅偙偺嬋柺忋偵擟堄偺揰P傪庢傝丄偦偺嵗昗傪倶偲偡傞丅偦偟偰丄偦偺揰俹偵偁傞儀僋僩儖傪倁偲偡傞丅 丂丂丂丂丂 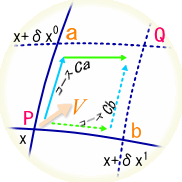 旝彫嫍棧偺兟倶0,兟倶1棧傟偨Q傑偱丄僐乕僗C倎丆僐乕僗C倐偺偦傟偧傟偱丄倁傪暯峴堏摦偝偣偰傒傛偆丅 僐乕僗C倎 丂揰倎傑偱倁傪暯峴堏摦偝偣傞丅 丂丂 偝傜偵丄俹揰傑偱暯峴堏摦偝偣傞偨傔丄埲壓偵幃偵倁乮倎乯//傪戙擖丅 丂丂 丂丂 丂丂 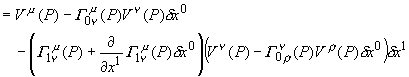 僇僢僐傪揥奐丅丂倁傪妵傝弌偡弨旛偺偨傔倁偺僟儈乕僀儞僨僢僋僗傪兿偵摑堦丅 丂丂 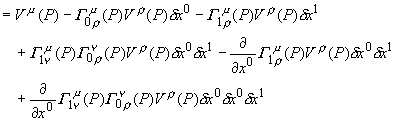 嵟屻偺崁偼旝彫検兟倶0偺擇師傪娷傓崁偱偁傞偐傜柍帇偡傞丅 嫟捠崁傪妵傝弌偟偰惍棟偡傞丅 丂丂 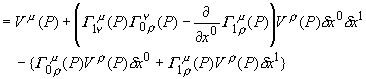 嵟屻偺乷乸撪偼僐乕僗懳徧偺崁偩丅 僐乕僗C倐 揰倐傑偱倁傪暯峴堏摦偝偣傞丅 丂丂 埲壓偺幃偵戙擖丅 丂丂 僐乕僗Ca偲摨條偵惍棟偟丄埲壓偺幃傪摼傞丅 丂丂 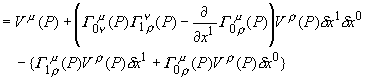 僐乕僗倎偺寢壥偐傜僐乕僗倐偺寢壥傪堷偔丅 丂丂 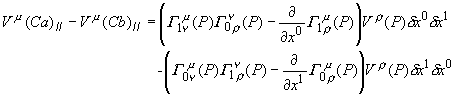 丂丂 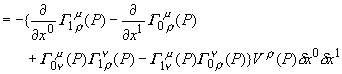 丂丂 傗偼傝丄嬋棪俼偼儀僋僩儖偺廃夞暯峴堏摦偵娭偡傞僥儞僜儖偩偭偨丅 兟倶0兟倶1偺崁偼僐乕僗倎丄僐乕僗倐偱埻傑傟偨柺愊偵懳墳偡傞偐傜丄廃夞僐乕僗偺埻傓柺愊偑戝偒偄傎偳丄儀僋僩儖偺曄壔偑戝偒偔側傞偙偲傪堄枴偡傞丅 偮偄偱偵丄僐乕僗傪傂偭偔傝曉偡偲丄 丂丂 偲側偭傞丅丂愭傎偳偺儀僋僩儖堏摦偺寁嶼弴斣偑媡偵側傞偐傜丄寢壥偼儅僀僫僗偲側傞丅丂 丂丂 偙偺嬋棪僥儞僜儖偼怓乆偲懳徧惈偑桳傝偦偆偩側丅傕偆堦搙丄椙偔幃傪挱傔偰傒傛偆丅 丂丂 偍偭両丂傂傜傔偄偨偧両丂偙偺僋儕僗僩僢僼僃儖婰崋偺慻傒崌傢偣偐傜丄 丂丂 偲偄偆丄柺敀偄娭學偵側偭偰偄傞傒偨偄偩丅 傕偭偲怓乆桳傝偦偆偩偗傟偳丄偝偡偑偵僕乕僾偱憱傝捠偟偩偭偨偺偱彮乆旀傟偨丅丂偲傝偁偊偢偙偙傑偱偲偟偰丄屻偼傑偨偺婡夛偵丅 丂丂 |
偲偙傠偱丄儊僀偺幚尡傗暘愅偼丄擇師尦嬋柺忋偺暔棟嬻娫偱偺偙偲偱偟偨丅丂偟偐偟丄偙傟傜偺摴嬶棫偰偼丄崅師尦拞偺擇師尦嬋柺偱傕傎偲傫偳廋惓偣偢偵巊偊傑偡丅
丂嶲徠暥專丒恾彂丂乮俀乯戞嘫復偱偼忋婰媴柺嵗昗倶偱偺儀僋僩儖傪兟倶偱堏摦偝偣偨応崌偺俼偲偺娭學幃偲偼暿偵丄嵟弶偐傜捈愙丄崅師尦撪嬋柺僷儔儊乕僞倳丄倴傪巊偭偰儀僋僩儖偺堏摦斖埻偺柺愊偲俼偺娭學傪摫弌偟偰偄傑偡丅埲壓偺悢幃曄宍傕娷傔杮彂傪嶲峫偵偟偰偄傑偡丅丂惓妋偵棟夝偡傞偨傔偵偼杮彂偺嶲徠傪偍彠傔偟傑偡丅
椺偊偽丄X嵗昗偱昞偝傟傞係師尦儕乕儅儞帪嬻撪偺擟堄偺嬋柺S傪峫偊傑偟傚偆丅S偼嬋慄孮倳,v傪巊偭偰峔惉偱偒傑偡丅偮傑傝丄倳,倴僷儔儊乕僞傪巜掕偡傞偲丄俽偺擟堄偺揰偑倶兪乮倳,倴乯偲昞偣傑偡丅
丂丂丂丂丂丂丂
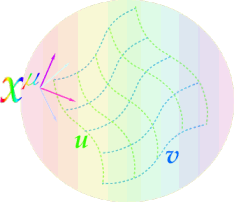
偙偺帪嬻撪慡堟偺寁検倗偑寛傑偭偰偄傟偽丄慡堟偱嬋棪俼偑寛傑偭偰偄傑偡丅
偄偪偄偪嬋柺俽偺寁検偐傜弶傔偰俽偺嬋棪俼傪媮傔傞昁梫偼柍偔丄儊僀偺幚尡偲摨條丄偙偺帪嬻撪偺擟堄偺嬋柺俽忋偱儀僋僩儖偺廃夞堏摦幚尡傪峴偆偙偲偑壜擻偱偡丅
偮傑傝丄帪嬻傪偁傜備傞妏搙偐傜抐憌嶣塭傪峴偆偙偲偑壜擻偩偲尵偆偙偲偱偡丅偦傟偵懴偊傜傟傞偩偗偺榗忣曬傪偙偺儕乕儅儞嬋棪俼偼曐桳偟偰偄傞偺偱偡丅
偦偺偨傔偺廋惓偼偛偔娙扨偱丄嵟弶偺幃
丂丂
偱丄兟倶0偲捈愙巜掕偟偨曄悢傪
擟堄偺嬋柺偵懳墳偡傞偨傔丄儭偺堏摦嵗昗幉巜掕梡偺僀儞僨僢僋僗傕兛偲妱傝怳傝傑偡丅
丂丂
摨條偵倶1傕
埲崀丄儊僀偑傗偭偨偺偲慡偔摨偠寁嶼庤弴偱堦斒幃偺
丂丂
傪摼傞偙偲偑弌棃傑偡丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂嶲徠暥專丒恾彂丂乮俀乯偺嶲峫斖埻廔椆