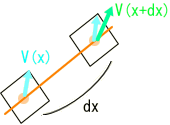
やれやれ、Dr.メイの一人よがりは相変わらずですね。 しかし、メイのおかげで測地線に基づく接続が定義できた様です。 リーマン空間における微分の定義に移る前に、メイの実験結果をもう一度整理しておきましょう。
平らな空間で、ベクトルAを直線、つまり測地線に沿ってPからQに平行移動させた場合、
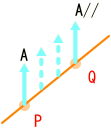
この様に、なります。ベクトルと線との角度は移動しても変わりません。
同じく、平らな空間で、ベクトルAや、Pにおける接線ベクトルBを曲線に沿って平行移動させた場合です。
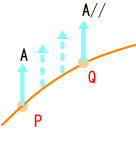
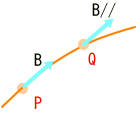
この様に、なります。 この場合ベクトルと線との角度は移動にともない変化します。 しかし、これも平らな空間では納得できます。
移動しても角度が変わらないようにすると、このようになります。
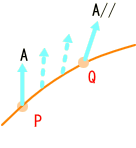
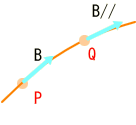
平らな空間で任意に引いた、何の意味も無い曲線に、こんな平行移動を定義する必然性は無いですね。
次に、曲がった空間（リーマン空間、正確には距離の定義が異なっているので擬リーマン空間）での平行移動だとしたら、どうなるのでしょうか？ 4元ベクトルの代表選手として、4元速度Vで実験してみました。4元速度ベクトルの平行移動も、他の4元ベクトルも同様に平行移動が定義されるはずですから。
まず、平らな時空間（ミンコフスキー時空）での直線、つまり測地線に沿った4元速度ベクトルの分布状況です。 線素ｄｓとV･ｄτは一致します。
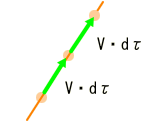
各線素の傾き、および巾は一致しています。 ですから、線上に分布する４元速度ベクトルも各々一致し、同じ成分を持っています。
どこかのVを『平行移動』させても、直線上の別のベクトルに重なります。 重要なことは自由落下系もミンコフスキー時空なので、このベクトルの平行移動時の『挙動』が当てはまるということです。
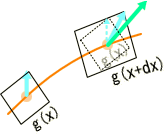
次にこれを重力場からながめて見ましょう。先ほどの直線は、曲がった空間での測地線として見えます。測地線は、質点の自由落下線です。
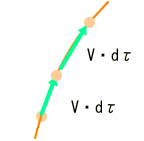
平らな時空の場合と同じく、曲線を構成する線素ｄSとV・ｄτは、一致しています。
そこで、先ほどのベクトルの平行移動の『挙動』を再現させるとどうなるのでしょうか？
結局、『ベクトルVを測地線に沿って平行移動させると、線素と重なりながら移動します。大きさも線素に比例します』ということになります。
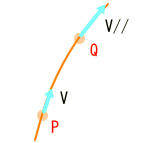
この平行移動は、Pを（ｘ）、Qを（ｘ＋ｄｘ）とすると、測地線方程式から導かれたクリストッフェル記号を接続として用いて、
と定義できました。
当然、４元ベクトル以外の任意の4元物理ベクトルAも、同一の接続係数を使って平行移動が定義されます。
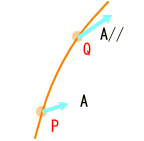
よし、接続が決まった。 これで、物理法則の記述にやっと微分が使えるようになる。 微分が出てこない物理法則なんて聞いたことがないからな。
が定義できたからベクトルの微分を
