�@���C�̓��[�}���w�������̂��ƌ����āA���Ȃ��Ȃ��Ă��܂��܂����B���ꂩ���ɐi�ނ��߂ɂ͕K�v�Ȃ��̂Ȃ̂ł����A�T�{���Ă����悤�ł��B�����ŁA���B�����������܂��傤�B�@���ꂩ���͏��X�����������Ȃ�܂��B�@���������ΐ����_�𗝉������ł͕K�v�ɂȂ鐔�w�ł��B
�Q�D�R�D�P�@���[�}���w
�@�����n�ɂ���܂鎞��̓��[�����c�ϊ��ŁA�ʂ̊����n�Ŏw�肳��鎞��ɕϊ�����܂��B
�@�@�@�@�@�@�@�@�@�@�@�@�@���[�����c�ϊ���
�@�@�@�@�@�@�@�@�@
�@�@�@�@�@�@�@�@�@�@�@�@�@���[�����c�t�ϊ���
�@�@�@�@�@�@�@�@�@
�@�@�@�@�@�@�@�@�@�@�@�@�@�A���A
�@�����Ă��̎��͉��̗�Ō����ƁA�̊����n�̎���Ԃ����݂��A�̌n������ۂɑ��������ƃ��[�����c�ϊ��Ŏ������ʂ�A�������k��Ŏ��Ԃ��x��Ă���ƌ������ł��B
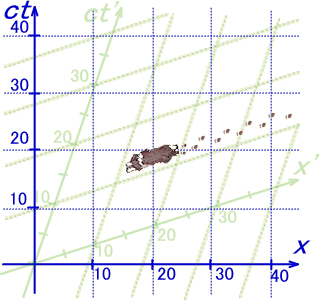
�����Ă��̎��́A�����Ɂw�قȂ鎞��Ԃ����݂���x�Ƃ������Ƃł��B
�����ƌ����Ɓw�قȂ�n�͕ʐ��E���x�Ƃ������Ƃł��B�@������ƒ����I�ȕ\���ł����A���ԂⒷ���̊���قȂ��Ă��܂��킯�ł�����A�w�ʐ��E�x�Ƃ��\�����A���Ȃ����O��Ă͂��Ȃ��̂ł͂Ȃ��ł��傤���B
�K���Ȏ��ɁA���̎���Ԃ͍��W�����Ό����Ă��邾���ŁA�i���łɊԉ��т��Ă��邾���Łj�����̍��W�n�ŕ\�����Ƃ������܂����B
�Ƃ��낪�A��قǂ̃��C�̎����ŕ�����悤�ɁA�d�͂��e�����鎞��ɂ����ẮA���Ȃ��Ƃ������̍��W�ŕ\��������Ȃ����Ƃ����͊m���ł��B

�G���x�[�^�[�̒��Ő^�����������Ă��郁�C���A�^�������i��ł�������A�n��̏d�͏�ɌŒ肵���n����݂���A���̎���Ԃ͋Ȃ����Ă����������ɂȂ�܂��B�G���x�[�^�̒��͋Ǐ��I�ȃ~���R�t�X�L�[����ł������͂��Ȃ̂ł����B
����ɋt���������������A���C�̎��R�����n���猩���d�͌n���Ȃ����Ă��鎖�ɂȂ�܂��B
���̗l�Ȃ��Ƃ̓��[�����c�ϊ��ŕ\���ł��܂���B�����ŕK�v�ɂȂ��Ă��鐔�w�̓���ĂƂ��āA�Ȃ�������Ԃ�\�����郊�[�}���w���K�v�ƂȂ��ė���̂ł��B
�Q�D�R�D�Q�@�[���[�N���b�h��Ԃ��烊�[�}����Ԃ� �@�@�@
�S���������͈قȂ銵���n�ԂŁi����ɐ��f�ł���A�Ȑ����W�ŕ\������ʍ��W�n�ɑ��Ă��j�s�ςł����B�@����𗘗p����ƁA�����n�Ɠ����ł��鎩�R�����n�����Ƃ��āA�d�͏�̍��W�����m��ł������ł��B
�@�����A���R�����n���g���Č��܂��傤�B�@�܂����B�͏d�͏ꑤ�̎���i��ct�CX�̍��W�j�ɐÎ~���Ă�����̂Ƃ��܂��B�@���̏d�͏�͔��ɑ傭�A���ꂩ��c�_����͈͂ł͈�l�ɕ��z���Ă�����̂Ƃ��܂��B
���̏d�͏��X�����Ɏ��R�������鎿�_���l���Ă݂܂��傤�B�@�}�ł͂n����A�o�ւ̐��E���ŕ\����܂��B
�@���_����L�тĂ���Ԃ��x�N�g�����S�����x��\���܂��B�����Ƃ�����̐����ł͎��Ԏ��Ƌ�Ԏ��w�́h�Q���h�Ȃ̂ł��傤���A�S���Ƃ́w���Ԏ��ƍ��킹�āx�Ɨ����肢�܂��B
�@�n�_���玩�R�������n�߂܂����B�������ŏ��̃j���[�g���͊w�ł̑��x�̓[���ł��B���������ΐ����_�̂ł�4�����x�u�̏ꍇ��
�@�@�@�@�@�@�@�@�@�@�@�@�@�u����������/����
�ƒ�`����܂��B
�т͌ŗL���ԂƌĂ�A�̎��R�����n�̎��Ԃ��f�̂��Ƃł��B�������A���f�͈ꗥ�ł͂Ȃ��A���_�̉^�����x�ɂ���ĕω����܂��B�܂莿�_�������ʼn^������ƁA������莞�����ނ悤�ɂȂ��ł��B
����4�����x�̒�`�ł́A�����Ƃ��Ă��Ă��A����Ԃ̒��Ŏ��ԕ����ɓ����Ă��邱�ƂɂȂ�܂��B�����Ƃ��Ă��鎿�_�̌ŗL���Ԃ͂�����̌n�Ɠ������Ԃ����݂܂��B
�܂肄�с������ł��邩��
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�u0������0/����
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@��C����/����
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@��C
�ƂȂ�A���̏ꍇ�̂S�����x��C�ɂȂ�܂��B
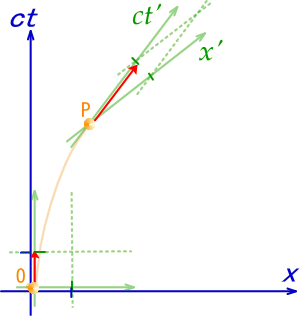
���Ԃ��o�ɏ]���A�d�͂ʼn�������w�����̑��x������ė��܂��B
O����P�ɂ�����o�H�͂P�{�������݂��܂���B������X�����ɏ����x���������Ă݂܂��傤�B
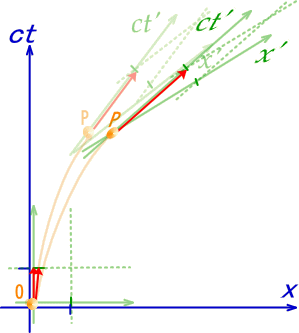
���̂悤�ɓ��B�_���E�ɂ���Ă��܂��܂��B��l�ȏd�͏�ɂ����鎩�R�����̐��E���͋Ȑ��ł͂���܂����A�B��P�{��������܂���B�K���Ɉ������Ȑ��ɉ����Ď��_���ړ������邱�Ƃ͕s�\�ł��B���͂��̐��͑��n���ƌĂ�A�Ȃ���������ɂ����钼���̖����������܂��B
�@�ǂ����Ă��ꂪ�����̑��ɂȂ�̂��ł����āH�@�����ł��ˁA�܂����C�Ɏ��������肢���Č��܂��傤�B
 �@�ȂA�ȂB�@�ӂ��[�����B�@�������ǂ��������āE�E�E�H�@���܁A���[�}���w�Ȃ���̂̕����łƂ��Ă������������́B�@�t�������Ă��鎞�ԂȂ����B�@�ӂ�B �@�ȂA�ȂB�@�ӂ��[�����B�@�������ǂ��������āE�E�E�H�@���܁A���[�}���w�Ȃ���̂̕����łƂ��Ă������������́B�@�t�������Ă��鎞�ԂȂ����B�@�ӂ�B
�@���H�@�悾�ꂪ�A����Ă���āH�@�E�E�E�����A��������Q������Ă��̂��o�������B�@ ���[��B�@���傤���Ȃ��ȁB�@�C���]���Ɏ����ɕt�������Ă�邩�B ���X�B���̋Ȃ����Ă��鐢�E�B�̂ǂ����^�������Ȃ̂������āH�@���[�ށB�@�����ǂ����Ă��^�������ɂ͌����Ȃ��ȁB �������A����Ԃ̍��W�ڊώ@���邱�Ƃ��o����A����I�Ȏ������u���L�����B�@�����A�w���C�̎���ԍ��W�P�ʃx�N�g���\�����u�x���B�@���쌴����Y��Ă���Ƃ����Ȃ��̂ŁA��ɐi�ޑO�ɍēx���K���Ă����悤�ɁB �@�@�@�@  �@�����B�@���炭�g��Ȃ��ł�������A�܂��͎���ԕ\�����u�̓���m�F�B �d�̖͂����F����ԂɁA���̑��u�Ǝ��_�Ƃ��ꏏ�ɐÎ~�����Ă����B�������Î~���Ă���A���C�J�����ő��肵�Ă݂悤�B �@�@�@ 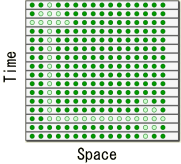 �悵�悵�A�����Ɠ����Ă���悤���B�@���Ԏ��i���j�A��Ԏ��i���j�̒P�ʃx�N�g�������s������Ԃʼnf���o����Ă���B ������A������x�A�A���������Ԋϑ�����ƁA�L�掞��}�Ƀv���b�g���鎖���o����B ���̐}�̗l�ɃA���C�J�����͋�Ԏ���1�ɉ����Ă�����ƕ��ׂĂ���B����͐n�̍L���ԍ��W���̂��̂Ƃ�������B �@�@�@�@�@�@�@ 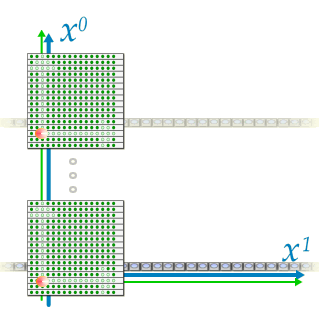 ���_�y�ю���\�����u����ʂ̊����n�Ƃ��ėŕ\���ƁA��̐}�̗l�ȊW�ƂȂ�B ���́A�ړ������Ă݂悤�B�@�܂�A�Ɨ͐Î~�n�ƈړ��n�Ƃ������ꑊ�ΐ����_�I�ȊW�ƂȂ�B  �@�A���C�J�����̐Î~�n�i�j�ɑ��āA�̌n�������Ɉړ������Ă݂�B ����[�B �@�@�@�@�@ 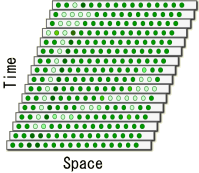 ���āA�ǂ����ȁH �����I�@�����ƈړ��n�̎Ό������f���Ă���B �������͂�A�L��ɓn��J�����摜������}�ɏd�˂Đ������Ă݂悤�B �@�@�@�@�@�@�@�@�@�@ 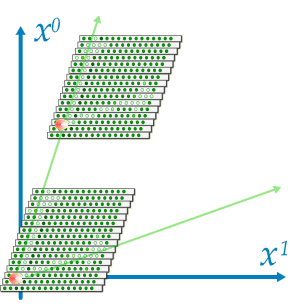 �����n���m�̍��W�����L��ɉ������Ă��A�ړ��n�̎Ό����̌`��ɂ͓��R�ω��͖����B�@�ǂ��ɂ���A���C�J�����ŎB�e���Ă����ʂ͓������B �ȏ�Ŏ���\�����u�̓_���ƁA���[�����c�ϊ��ɂ����铪�̐��������B ����ł́A���́w���C�̎���ԍ��W�P�ʃx�N�g���\�����u�x�E�E�E�B�������������O�������X�A�����B�悵�A����\�����u�Ɨ������B���̎���\�����u���G���x�[�^�[�ɐςݍ���Ŋϑ����Ă݂�B
���ǁA���_�͂҂���Ƃ������Ȃ������B������̏d�͌n����̊ϑ��ł͂ǂ��Ȃ��Ă��邩�ȁH �@�@�@�@�@�@�@�@�@�@ 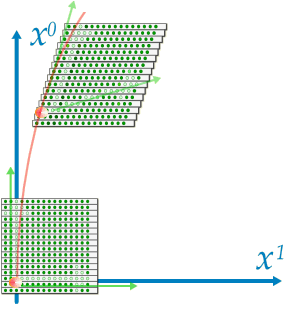 �G���x�[�^�̒��̎���́A���x���t���ɏ]�����W�������čs���Ă���B����ƍ��킹�Ď��Ԏ��̃x�N�g���͏��X�Ɋԉ��т��Ă���B ��I�@�������A�v���o�����B���̃x�N�g���̓G���x�[�^����ł̎��Ԏ����\������P�ʃx�N�g���������B �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@  ��������̗l�ɂȂ��Ă����ƁA���R��������G���x�[�^�̎��Ԏ����ǂ̂悤�ɕω����Ă���̂����v���b�g�ł���͂��B �悵�A����Ă݂悤�B �܂��A�G���x�[�^�̒��̍��W�n�ŁA���_��\���ƁA���̗̍��W�̒ʂ�ƂȂ�B �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ 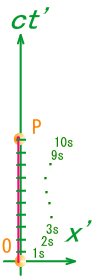 ���ɁA�̏d�͏�n���W��ɁA����ɑΉ�����G���x�[�^�[�̎��Ԏ����v���b�g���Ă݂�B �@�@�@�@�@�@�@�@�@�@�@�@�@�@ 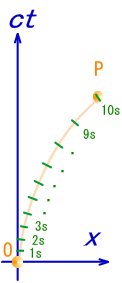 �ӂނӂށB�@���x���t���ɂ����W���̎��ԊԊu���ԉ��т��Ă����̂�������B �Q�D�R�D�R�@���n�� ����ɏڂ����ϑ����邽�߂ɁA���v�ƂƂ��Ɏv�����Ă��̎��_�ɏ�������ė��������Č��悤�B�@�G���x�[�^�̊O�ɏo�ė���������̂́A���X�|���C������̂����B �@������荇���������̂́A���Ԏ��F��0�f�ɉ������l������C����'�i=C���сj�ł����Ȃ��B�@���_�ɂ�����������v�����炻���炩�猩����A�ŗL���Ԃƌ������ɂȂ�B 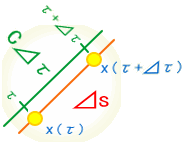 ������A�����炩�璭�߂Ă���ƁA��̐}�̗l�Ɏ��_�̐��E���ɂӂ�ꂽ�������̂悤�Ɍ�����B ���̃������̊Ԋu����'�i���сj������\�����u�ő���P�ʎ��Ԃ̂O�D�Q�S[���b]�Ƒ����悤�B �@ 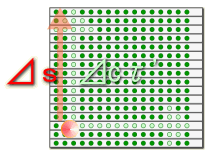 �@�@�@ �@�@�@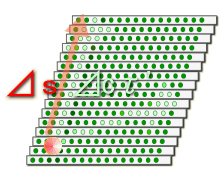 ����ɂ��A����\�����u�̒P�ʃx�N�g�����Ȃ��ČŗL���Ԃ�\���ł��� �@�@�@�@�@�@�@�@ 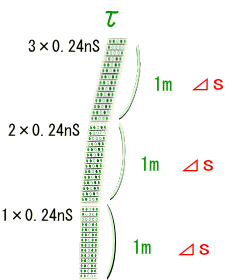 ���������̎��R�����n�ł̂P���̐߁X���̏d�͌n���W���̂ǂ̈ʒu�ɑ�������̂����A�܂���X�͒m��Ȃ��B �������A4���������̓�懙��2�͊����n�Ԃŕs�ϗʂł������B�@�P���ƌ��������͋�Ԃ̋Ȃ���ɑ��\�������ȋ������Ƃ���B��������Ƒo�����Ǐ����[�����c�n�ƌ��Ȃ��A�R�����n�̋����̓�悪�P��2�Ƃ����ł���A�d�͏�n�ł��P��2�ƂȂ�͂����B �܂�A���̔����ӂ̏d�͏�n���W�Ƃ̊W�͈ȉ��̗l�ɕ\������B �@�@�@�@�@�@�@�@�@����2=���ʃ�(x)��x����x��=1[m2] ����ɁA��قǂ̔��ϕ��ɂ���͂ɔ����A����2����f����2�Ƃ��悤�B���̏ꍇ���A�ȉ��̗l�ɔ��������Ɠ��l�̊W�ŕ\�����B 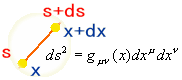 �������A�d�͏�ɂ�����v�ʂ��i���j�͍������m�ł���B �����Ŏ��̂悤�ɉ��肵�悤�B �@�@�@�w�d�͏�ɂ����鎿�_�̋O�Ղ͍ő勗���ł���x �ȉ��ɂ��̉���Ɏ��鐄�_���q�ׂ�B 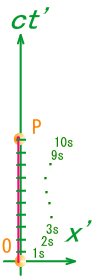 ���̐}�̗l�Ɏ��R�����n�ł�O-P�Ԃ̂��ő勗���ł������B�ܘ_���̋O�Ղ͒����ł���A���B��1�{�ł���B  �d�͏�ɂ��������_�̋O�Ղ��B��1�{�����Ȃ������B�䂦�Ɂw�d�͏�ɂ�����O-P�Ԃ͍̂ő勗�������x�Ɖ��肷�鎖�͎��R�ł���B �ȉ����̉������ɏd�͏�ɂ����鎿�_�̋O�Ղ����߂Ă݂�B ���̐}��x1�Cx2�̋�ԓ��̂���x2�����Ɋ����^�������Ȃ���x1�̕����ɏd�͂������������Ă���l�q�������Ă���B ���̋O�Ղ̏�̔C�ӂ̓_�����A���Ƃ���B 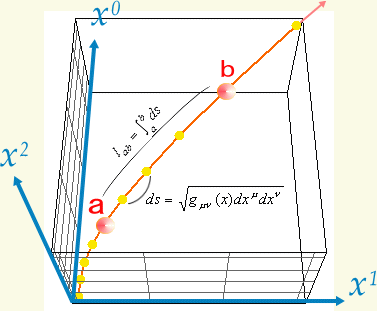 �O�Ղ̈ʒu���w�肷��p�����[�^�Ƃ��ċ�������p�����A����Ԃ�ϕ�����B �@�@ ���̒l�����C���ۊԂ̋������B�@ ���̎��A���͂ǂ�Ȍ`������Ă���̂��낤���H�@���̌`��͂����g�̊����i���j�Ƃ��Ăƕ\�����B�@ 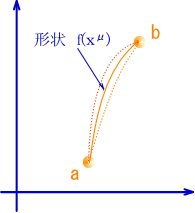 ����ɋ�������l�i���i���j�j�Ƃ����悤�Ɋ�����ϐ��Ƃ������ƍl������B 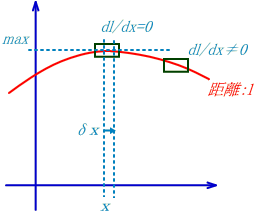 ������������Ă��鎿�_�ł̂��A���ԋ����́A���R�����ł���A�ő�l�i�~���R�t�X�L�[����ł̂S������������Ԏ��̕������}�C�i�X�ł��邽�߁A�ŏ��l�ł͂Ȃ��ő�l������j�ł���B ������������Ă��鎿�_�ł̂��A���ԋ����́A���R�����ł���A�ő�l�i�~���R�t�X�L�[����ł̂S������������Ԏ��̕������}�C�i�X�ł��邽�߁A�ŏ��l�ł͂Ȃ��ő�l������j�ł���B�]���āA���ʂœ��l�ł�����f������ςݏd�˂đ������d�͏ꑤ�ł̒��������A�ő�l�łȂ���Ȃ�Ȃ��B �܂�A���m�̂��i���j�́A�����ό`���ŋ����F�� �̕ω����O�ƂȂ�ɒl�̏��������Ȃ���Ȃ�Ȃ��B�@�ȉ����̋ɒl�����𑫂�����Ɏ��_�̌o�H����̓I�ɋ��߂Ă������B�@�Ȃ��ό`�́A���_�Ƃ��_���Œ肵�āA�r���̌o�H�����炩�ɕό`������̂Ƃ���B �@�@�ȉ��̐����ό`�̑�́@�Q�ƕ����E�}���@�i�S�j�@���Q�l�ɁA�����Ǝ��̏ڍוό`���Ԃ��܂����B �@�C�ӂ̌o�H��I�сA���̌o�H�`��ɔ����ό`����^�����ꍇ�A�����̔����ω������ł������Ƃ���B ���̏ꍇ�A�o�H��ɂ�����e���f �@�@ �� �@�@ �ƂȂ�B ���ӂ��ꂼ���W�J���悤�B�����������ό`�ł̋ɒl�������v�Z����̂�����A���A���̂Q���ȍ~�̍��͖����ł���B �@�@ �A���_�[���C�������������͕ό`�O�̓������B�c��̍����ό`�Ő��������ł��邩��A���̕����������o���ƁA �@�@ ����ɁA�E�ӂ���f�̔����ω��݂̂̍��ɂ���B �@�@ 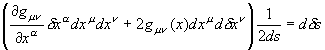 ����̂��]���ԑS�o�H�ɂ킽��ϕ����Ƃ�ƁA�����ό`���̋����ƂȂ�B �@�@ �����ŏ�L�̋ɒl��������/����=�O���A �@�@ ��Q���� �@ 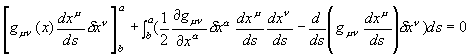
��P���� 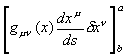 �͊��炩�ȕό`�Ƃ��������i�܂藼�[�͕ό`���Ȃ��j���痈����i���j=���i���j=0�ɂ��O�ƂȂ���������B����ɂ����ɂ��ς̔���*1��W�J���� �͊��炩�ȕό`�Ƃ��������i�܂藼�[�͕ό`���Ȃ��j���痈����i���j=���i���j=0�ɂ��O�ƂȂ���������B����ɂ����ɂ��ς̔���*1��W�J�����@�@ 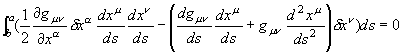 ���ƃ˂̃C���f�b�N�X�����킹�ăJ�b�R�̊O�ɂ����肾���B �@�@ �����ό`���͔C�ӂł��邩��A�������������邽�߂ɂ́A��ϕ������O�ɂȂ�Ȃ���Ȃ�Ȃ��B�@����āA �@�@ ���g���b�N�e���\�� �@�@ �@�@ ����/�����̍�������o�����߂ɃC���f�b�N�X������B �@�@ �@�@ �@�@ �ƂȂ�A�ȉ��̉^����������B���ꂪ���n���������ƌĂ����̂ł���A�Ȃ�������Ԃł̒����̑���ɂȂ���̂��B �@�@ �������@ �@�@�@�@�@�@�@�@�@�@�@�@�@�Q�ƕ����E�}���@�i�S�j�̎Q�l�͈͏I�� �@���̂悤�ɑ��n���͏d�͏�̌n�ł͍ŒZ�o�H�ł���B�����ďd�͂����������R�����n��A�d�͂̉e���̖��������n�ł́A�ŒZ�o�H�ł����ɂ���ɓ��ʂȁh�����h�ɂȂ�킯���B �Q�D3�D�S�@�x�N�g���̕��s�ړ� �@�����܂ŗ�����A���łɐڑ��ƃx�N�g���̕��s�ړ��Ɋւ���������B �S�����x�͑��n���̐ڐ��x�N�g���ł���B���R�����n�̗���ł͒����ɉ����āh�ڐ��x�N�g���h��ڐ������Ɍp�������Ă����B�܂��Ƀx�N�g���̕��s�ړ����B �@�@�@�@�@�@�@�@ 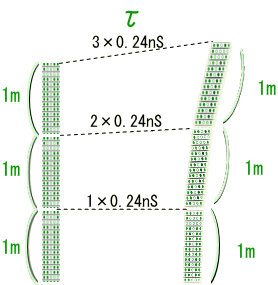 �@������d�͏�n�̗���ōl����B���_�̗����O�Ղł���Ȑ���̑��n��������A���̋Ȑ��̐ڐ��ɉ����ĂS�����x�x�N�g�������s�ړ�����̂߂Ă����ƌ������ƂɂȂ�B 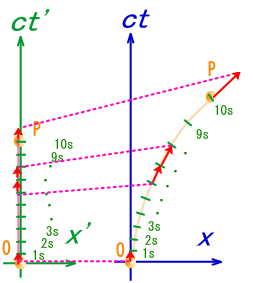 ���R�����n�@�@�@�@�@�@�@�@�d�͏�n�@�@�@�@�@�@�@�@�@ �@�Ƃ���ŁA�����𗣂ꃊ�[�}���w�ɂ�����x�N�g�����l����B���̏ꍇ�A���s�ړ��̒�`�͏����ɐ��w�̖��ƂȂ��`����ŐF�X�Ȑ����������w��̋�Ԃ��n���ł���B ���A�n�Ƃo�̊Ԃ��ڋ߂��Ĕ������������ł���Ƃ��悤�BVo�����s�ړ����ꂽ���ʃx�N�g���u���ƂȂ�������� �@�@ �̂悤�Ȍ`�ŕ\�������B�܂蕽�s�ړ�����Ƌ��������ɔ�Ⴕ�Ĉړ��O�̃x�N�g���̐����ɑ��A�ړ���̃x�N�g�������Ɉ��̕ω���������B ���̒��łR�����}�g���b�N�X�̂w�͐ڑ��W���ƌĂ�A��������ǂ���`���邩�ł���B �@�Ƃ���ŁA��X�̓��[�}���w�́A������Ԃɑ��鉞�p�ɂ��ċc�_���Ă���̂�����A�x�N�g���u�͉��炩�̕����ʂłȂ���Ȃ�Ȃ��B ����Ȃ�ΐ�قǑ��n�����\�������S�����x�x�N�g���ł����Ă��ǂ��͂����B �@�Ƃ������ŁA�u��4�����x�������Ƃ���B��������ƍ��ӁiVp��-Vo���j�͔����������u�Ă����x���Ɠǂ߁A���u�Ə����\����B����ɂ��тŗ��ӂ�����ƁA �@�@ �ƂȂ�A����� �@�@ �Ə�����B ����A���n���̕������� �@�@ �ł������B ������c����тł��邩��S�����x�̒�`�u������/���тɂ�� �@�@ �@�@�@�@�@�� �@�@ �@�@�@�@�@�� �@�@ �Ɛڑ��W���ƕ������قȂ邾���œ��l�̌`�ɕό`�ł���B�ڑ��W���Ƃ��ăN���X�g�b�t�F���L�����g���������ɂ��Ȃ��Ă��������B ���̕����ʁA�Ⴆ�A�_�́i���������Ɍ������j�����x�N�g���Ȃǂ͂ǂ����ȁH�@�l�����x�x�N�g�����������ʂȕ����ʂł���킯�������B���x�x�N�g���Ɠ��l�̕��s�ړ��̋K�����K�p�����ׂ����Ǝv���̂����B �@�悵�A������x��K�������ė����������B����I  �@�@�@�@�@�@�@ �܂��A��������̎���ԉ摜���B �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@  ��K�Ƌ�Ԏ��x�N�g���͈�v���Ă���B ���ɁA���炭�������đ��x���t���Ă������̉摜�����Ă݂悤�B �@�@�@�@�@�@�@�@�@�@�@�@�@ 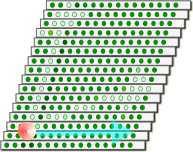 �����A��K�Ƌ�Ԏ��x�N�g���͂���Ă��܂��Ă���B����������K���x�N�g���Ɍ�����悤�ɁA�������ɖ�K���������Ă������̂ɁB �����4���x�N�g���ł͖����ƌ������̂��ȁH �E�E�E�m���ɁA���̒�K�̓��[�����c���k���Ă���B�@���k����͈͂͋�Ԑ�����3�����̒��Ɍ����Ă���A���̒��ł��ړ������݂̂��B�@��������4�����x�x�N�g���Ƃ́A�����������Ⴄ�l���B 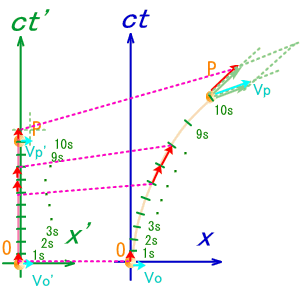 ���R�����n�@�@�@�@�@�@�@�@�d�͏�n�@�@�@�@�@�@�@�@�@�@�@�@�@�@ �x�N�g���̕��s�ړ��ł͂�4�����x�x�N�g���Ɠ����ϊ�����ƍl����Ə�̐}�̗l�ɂȂ�Ȃ���Ȃ�Ȃ��B���̂Ȃ�A�ڑ��W���ɃN���X�g�b�t�F���L�����g�������炾�B �܂�A4���ʑ��x�N�g���� �@�@�@�@�@�@�@�@�@�@�@ 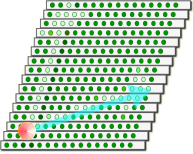 �̗l�ɁA��Ԏ��P�ʃx�N�g���Ɠ��l�ɕ��s�ړ�����ƌ������ɂȂ�B ���̗l�ȂS���x�N�g���̍l�����͓��ꑊ�ΐ����_�ł̃~���R�t�X�L�[����ɂ����镨���@�����\�z�����ł������R�ȋK��ł���B�@�S�����W���̕ϊ������[�����c�ϊ��ł���A���̑��̕����ʂƖ@�������l�ɕϊ��\�Ƃ������Ƃ����ꑊ�ΐ������ł��������炾�B ���ꂩ��\�z���悤�Ƃ��Ă���d�͏�̗��_�ł����n���ɉ�����4���x�N�g�������s�ړ����Ă��������ʁA���̏�Ԃŕ����@�������������L�q�o���邩�ǂ������d�v�ɂȂ�B �@���̂悤�ɕ����ʂ��S���x�N�g���ő����A���n���ɉ�����O����P�Ɏ��R����������B����s�ړ��̐ڑ��ƍl���A���̌��ʁA �@�@ �@�@ �ƂȂ�w���t�ړ��Ńx�N�g���̑傫���͕ω����Ȃ��x�Ƃ���������������������Ԃ��\�z�ł��邱�ƂɂȂ�B�����A���������������[�}���w����ɁB �ȂɁA�Q�Ă�������āH�E�E�E�B�@�ӂ�A���[�}���w�ł͍��������悤�Ƀx�N�g���̕��s�ړ��łǂ��Ȃ邩�ɂ��A���낢��ȋ�Ԃ��`�ł���B�@�����g�������Ď������Ċm���߂��B���̎��̎������炵�āA���̒�`����Ԃ����Ƃ��炵���B���n���̒��ł́A���ԃx�N�g������K�̒����x�N�g�����A����ɂȂ邮�炢�S�R�ω����Ȃ��������炾�B �@�҂Ă�A���̂��Ƃ��w���C�̓}�k�P�ł͖����̌����x�Ǝ��Ă��Ȃ����H �������A���̎��Ɠ������B���R�������Ă������́A�܂葪�n���̒����B�����Ē��ɂ��������A�F���D�̋Ȃ���ɋC���t���Ȃ��̂��}�k�P�Ȃ킯�ł͂Ȃ��A��������������B�O���猩�Ă����҂������Ԉ���Ă���̂��B������x�N�g���̒��������ɏ]���I����Ȃ������A���n�����ɏ]���I�Ƃ��������B ���ށB���s�ړ��̒�`�́A����Ɍ��߂��I�@�悤���A����Łw���C�̓}�k�P�ł͖����̌����x�Ɓw���C�̓h�W�ł͖����̌����x�A���̓�̈̑�Ȃ�w�������Ɋ�Â��S�F�����Ղ̖@��������B�����A���̎��̑s��Ȃ��]�̎������܂�����߂Â��ė����悤�ȋC�����邼�I�͂��͂��́B  |
 �O�b�A���_�������I
�O�b�A���_�������I �T�b�A�܂��܂��������I
�T�b�A�܂��܂��������I