‚PپD‚Wپ@ƒ~ƒ“ƒRƒtƒXƒLپ[ژ‹َ‚ئƒچپ[ƒŒƒ“ƒc•دٹ·
‚PپD‚WپD‚Pپ@ƒ~ƒ“ƒRƒtƒXƒLپ[ژ‹َ
پ@چ،‚ـ‚إژٹشژ²‚”‚ح[•b]‚ً’Pˆت‚ئ‚µ‚ؤ‚¢‚ـ‚µ‚½پBƒOƒ‰ƒt‚جˆê–عگ·‚ح‚P[‚r]‚ئ‚©‚P‚O[‚r]‚ئ‚¢‚¤—l‚ةٹ„‚èگU‚ء‚ؤگà–¾‚µ‚ؤ‚¢‚ـ‚·پB‚ـ‚½‹َٹشژ²?‚ج•û‚ح[‚چ]‚ً’Pˆت‚ئ‚µ‚ؤ‚¢‚ـ‚·پB ƒOƒ‰ƒtڈم‚جˆê–عگ·‚ح‚P‚b[‚چ]پi‚R‚O–œ‚j[‚چ]پj‚ئ‚©‚P‚O‚b[‚چ]پi‚R‚O‚O–œ‚j[‚چ])‚ئ‚µ‚ؤگà–¾‚µ‚ؤ‚¢‚ـ‚·پB
پ@‚±‚ê“™‚ج•\Œ»•û–@‚ح“ْڈي‰نپX‚ھٹµ‚êگe‚µ‚ٌ‚إ‚¢‚éژٹشپ]ˆت’uٹضŒW‚ج•\Œ»•û–@پiڈc‚ةڈ‘‚‚©‰،‚ةڈ‘‚‚©‚ح•ت‚ة‚µ‚ؤپj‚إ‚·پBگg‹ك‚ب‚ئ‚±‚ë‚إ‚ح—ٌژش‚جƒ_ƒCƒ„ƒOƒ‰ƒ€‚ب‚ا‚ھ—L‚è‚ـ‚·‚µپAƒjƒ…پ[ƒgƒ“—حٹw‚ج‹³‰بڈ‘‚إ‚à“¯—l‚ج•\‹L•û‚إ‚µ‚½پB
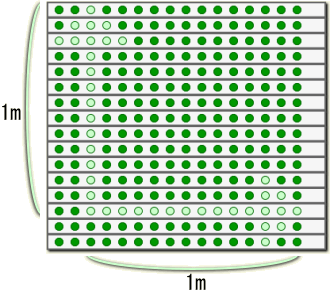
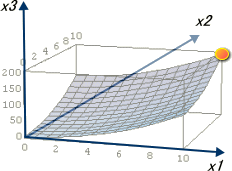
پ@گ}‚Qپ|‚P‚Q‚پ‚ج‚و‚¤‚ةپA‚P•bˆê–عگ·‚ة‘خ‚µ‚ؤ‚R‚O–œ‚j‚چ‚ًˆê–عگ·‚ئ‚µ‚ؤ‚¢‚é‚ج‚حپAŒُ‚ج‹Oگص‚ھ‚S‚T“x‚ة‚ب‚é‚و‚¤‚ةپAƒOƒ‰ƒtڈم‚إ•\Œ»‚µ‚½‚©‚ء‚½‚©‚ç‚إ‚·پB
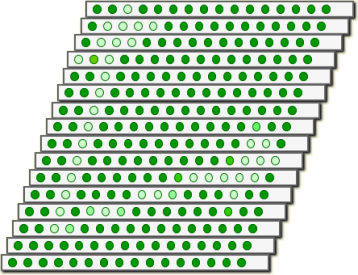
پ@‚ئ‚±‚ë‚إپAگ}‚Vپ|‚P‚Q‚‚“¯—l‚ةŒُ‚ج‹Oگص‚ً‚S‚T“x‚إ•\Œ»‚·‚é•ت‚ج•û–@‚إ‚·پB
پ@پ@پ@پ@
 پ@پ@پ@پ@پ@پ@
پ@پ@پ@پ@پ@پ@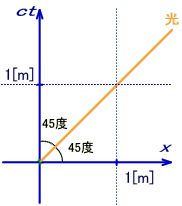
پ@پ@پ@پ@پ@پ@پ@پ@گ}‚Vپ|‚P‚Q‚پپ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@گ}‚Vپ|‚P‚Q‚‚
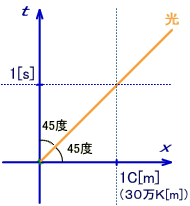
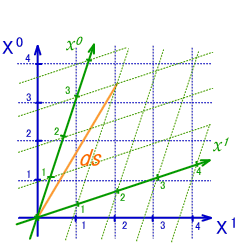
پ@‚±‚جچہ•W‚إ‚حپAژٹشژ²‚ة‘ٹ“–‚·‚éڈcژ²‚ھŒُ‘¬“x‚ƒ[‚چ/‚“]پ~‚”[‚“]‚إ‚ ‚èپAŒ‹‹ا‚ƒ‚”‚ح[‚چ]‚ئ‚¢‚¤‹——£‚ج’Pˆت‚ة‚ب‚ء‚ؤ‚¢‚ـ‚·پBپ@‚±‚ê‚حپw‚P‚چ‚ًŒُ‚ھگi‚ق‚ج‚ة•K—v‚بژٹشپx‚ئ‰ًژك‚µ‚ؤ‚‚¾‚³‚¢پBپ@‘ٹ‘خگ«—ک_‚إ‚حژ‹َ‚ً‚±‚جچہ•W‚إ•\Œ»‚µپAƒ~ƒ“ƒRƒtƒXƒLپ[ژ‹َ‚ئŒؤ‚ر‚ـ‚·پB
پ@ژٹشژ²‚ة‘ٹ“–‚·‚é‚à‚ج‚ھ‹——£‚ج‚ة‚ب‚ء‚ؤ‚µ‚ـ‚¢‚ـ‚µ‚½پB‚±‚±‚ةژٹ‚ء‚ؤ‚حپA‚ب‚ٌ‚¾‚©’ٹڈغ“I‚ة‚ب‚ؤ‚µ‚ـ‚¢‚ـ‚µ‚½‚ثپBپ@ˆبچ~پAژ‹َ‚ح‚±‚جپhگ³“”hپh‚ج•\Œ»–@‚إ‚ ‚éƒ~ƒ“ƒRƒtƒXƒLپ[ژ‹َ‚إ•\‚·‚±‚ئ‚ة‚µ‚ـ‚·پBپ@“––تپA“¯‚¶•¨‚¾‚ئٹ„‚èگط‚ء‚ؤ‰؛‚³‚¢پB
پ@ƒ~ƒ“ƒRƒtƒXƒLپ[ژ‹َ‚ة‚¨‚¯‚éگ¢ٹE“_‚إپASپ|S'ٹش‚ج‘خ‰ٹضŒW‚ًگ®—‚µ‚ؤ‚ف‚ـ‚µ‚ه‚¤پB
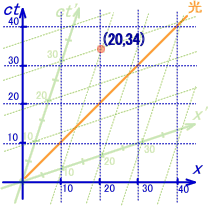
پ@گ}8-1‚ج“_‚حگأژ~ŒnپFS‚جچہ•W‚إ‘هژG”c‚ة
پ@پ@پ@پ@پ@پ@‹َٹشژ²پF‚Q‚Oپm‚چ]پ@پ@ژٹشژ²پF‚R‚S[‚چ]/‚ƒپà‚PپD‚Pپ~‚P‚O-‚V[•b]
‚ئ‚ب‚è‚ـ‚·پB
پ@“¯‚¶گ¢ٹE“_‚ًˆع“®ŒnپFS'‚إ“ا‚ف‘ض‚¦‚ؤ‚ف‚ـ‚µ‚ه‚¤پBپ@“¯—l‚ة‘هژG”c‚ة‚ح
پ@پ@پ@پ@پ@پ@‹َٹشژ²پF‚P‚Oپm‚چ]پ@پ@ژٹشژ²پF‚R0[‚چ]/‚ƒپà‚PپD0پ~‚P‚O-‚V[•b]
‚ئ‚ب‚è‚ـ‚·پB
پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ–ƒ}ƒEƒX‚ًڈd‚ث‚é‚ئS'چہ•W‚ً•\ژ¦
پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@
 پ@
پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@گ}8پ|‚P
‚PپD‚WپD‚Qپ@ƒچپ[ƒŒƒ“ƒc•دٹ·
پ@‚¢‚؟‚¢‚؟چہ•W‚©‚ç‘خ‰‚ً“ا‚فژو‚é‚ج‚ح‘ه•د‚إ‚·‚إ‚·پBپ@‚»‚±‚إ‚±‚جژ‹َگ}‚ًٹî‚ةپAS-S'‚جٹش‚جچہ•W•دٹ·ژ®‚ً‹پ‚ك‚ؤ‚ف‚ـ‚µ‚ه‚¤پB
”Cˆس‚جگ¢ٹE“_P‚ًSŒn‚جچہ•W‚ً—p‚¢‚ؤP(‚ک,ctپj‚ئ‚µ‚ـ‚·پB
پ@پ@پ@پ@پ@پ@
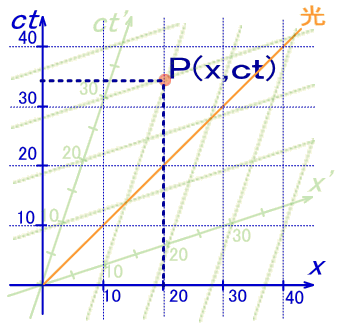
P“_‚ً’ت‚é‚جS'Œn‚إ‚ج“¯ˆêژچڈ‚ً“_گü‚إ•\‚µ‚ـ‚µ‚½پB‚ƒ‚”ژ²‚ئ‚جŒً“_‚ًT‚ئ‚µ‚ـ‚·پB
پ@پ@پ@پ@پ@
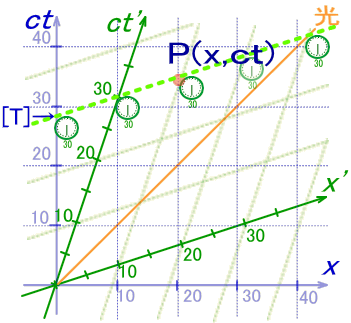 پ@پ@پ@پ@
پ@پ@پ@پ@ژں‚ة‚±‚ج“¯ˆêژچڈگü‚ًSŒn‚جچہ•W‚ًژg‚ء‚ؤ‚إ‹Lڈq‚µ‚ـ‚µ‚ه‚¤پB
پ@پ@پ@پ@پ@
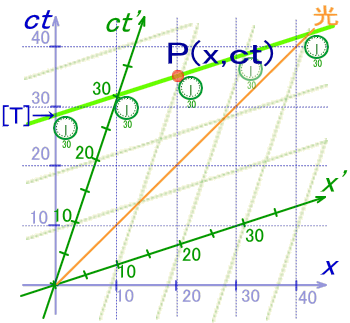
‚ـ‚¸پAT‚جSŒn‚إ‚جچ‚‚³پi=‚ƒ‚”چہ•W’lپj‚ً‹پ‚ك‚ـ‚·پB
پ@پ@پ@پ@پ@
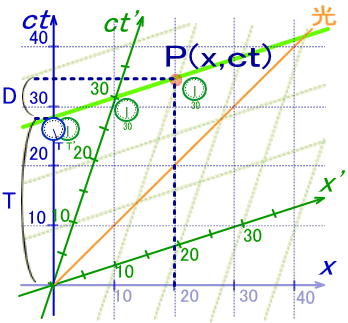
پ@پ@
ˆê•ûپActژ²ڈم‚إڈd‚ب‚éS'ŒnژچڈT'‚ئ‚جٹضŒW‚حگ}‚Vپ|‚P‚O‚و‚è
پ@پ@
پ@پ@پ@پ@پ@
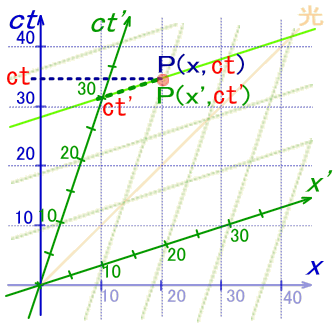
‚±‚ê‚ةگو‚ظ‚ا‹پ‚ك‚½
پ@پ@
‚ً‘م“ü‚·‚é‚ئ
پ@پ@
‚و‚ء‚ؤپA‹پ‚ك‚é‚”پf‚ج•دٹ·ژ®‚ح
پ@پ@
‚ئ‚ب‚è‚ـ‚·پB
“¯—l‚ةپA‹َٹشژ²‚ج‚کپf‚ةٹض‚·‚é•دٹ·ژ®‚ً‹پ‚ك‚ؤŒ©‚ـ‚µ‚ه‚¤پB
پ@پ@پ@پ@پ@
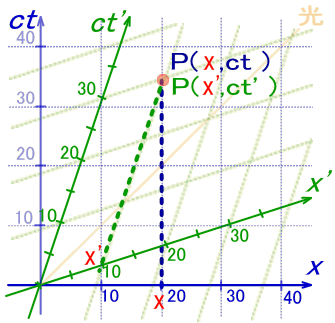
“±ڈo•û–@‚ح‚”پf‚جڈêچ‡‚ئ‘S‚“¯‚¶‚إ‚·پBپi‚ک‚ج•û‚ح‚ƒ‚ھٹ|‚©‚ء‚ؤ‚¢‚ب‚¢ژ–‚ة’چˆسپj
پ@
‹پ‚ك‚é•دٹ·ژ®‚ح
پ@
‚±‚ê‚”پf,‚کپf‚ج•دٹ·ژ®‚ً‚ـ‚ئ‚ك‚ؤڈ‘‚¢‚ؤ‚¨‚«‚ـ‚·پB‚±‚ê‚ھپA‚©‚ج—L–¼‚بƒچپ[ƒŒƒ“ƒc•دٹ·‚جژ®‚إ‚·پB
پ@پ@
پ@پ@
‹¤’ت‚جچ€‚ً
پ@پ@
‚ئ’u‚«پA‘¬“x‚–‚ةˆث‘¶‚·‚éƒءŒWگ”پiƒKƒ“ƒ}ŒWگ”پj‚ئ‚µ‚ؤپAٹ‡‚èڈo‚µ‚ؤ•\‹L‚·‚é‚ئپA
پ@پ@
پ@پ@
‚ئ‚ب‚è‚ـ‚·پB
‚ـ‚½پA‹t•دٹ·ژ®پiƒچپ[ƒŒƒ“ƒc‹t•دٹ·ژ®پj‚ح
پ@پ@
پ@پ@
‚ئ‚ب‚è‚ـ‚·پB‚±‚ê‚حپAS-S'Œn‚ج‘خ‰ٹضŒW‚حپA‰^“®•ûŒü‚جچ¶‰E‚ھ‹t‚ب‚¾‚¯پA‚آ‚ـ‚è‘ٹ‘خ‘¬“x‚ھپ{/پ|‚جچ·‚إ‚µ‚©—L‚è‚ـ‚¹‚ٌپBپ@ڈ]‚ء‚ؤپA‚کپA‚کپf‚ئپA‚”پA‚”پf‚ً“ü‚ê‘ض‚¦‚ؤ‘¬“x‚ًƒ}ƒCƒiƒX•„چ†‚ة‚·‚邾‚¯‚إپA‹t•دٹ·ژ®‚ً“±‚«ڈo‚¹‚ـ‚·پB
پ@گوپX‚جڈ€”ُ‚ج‚½‚كپAƒچپ[ƒŒƒ“ƒc•دٹ·‚ًچs—ٌ‰»‚µ‚ؤ‚¨‚«‚ـ‚µ‚ه‚¤پB
‚ـ‚¸ژn‚ك‚ةپAژٹشژ²‚ةچ‡‚ي‚¹‚ؤct‚ًˆê‚آ‚جژںŒ³‚ئ‚µ‚ؤˆµ‚¢‚ـ‚·پB
پ@پ@
پ@پ@
‚±‚±‚إپA
پ@پ@پ@پ@
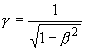
‚ئ’u‚‚ئ
پ@پ@
پ@پ@
‚±‚ê‚ًچs—ٌŒ`ژ®‚ة’u‚«ٹ·‚¦‚ـ‚·پB
پ@پ@
‚³‚ç‚ةƒچپ[ƒŒƒ“ƒc•دٹ·‚جŒWگ”•”•ھ‚ً“ٌژںŒ³‚جچs—ٌ‚k‚ئ‚µ‚ؤٹ‡‚èڈo‚µپAژw•W‚ً—p‚¢‚½گ¬•ھ•\ژ¦‚ة•د‚¦‚ؤŒ©‚ـ‚µ‚ه‚¤پB
پ@پ@
ƒAƒCƒ“ƒVƒ…ƒ^ƒCƒ“‚جڈk–ٌ‚ج‹K‘¥‚ًژg‚¢پAƒ°‚ًڈب—ھ‚µ‚ـ‚·پB
پ@پ@
‚±‚ج‹K‘¥‚حپwˆê‚آ‚ج‚جچ€‚ة“¯‚¶ژw•WپiƒCƒ“ƒfƒbƒNƒXپj‚ھ“ٌ“xڈ‘‚©‚ê‚ؤ‚¢‚½‚çپA‚»‚جژw•W‚ةٹض‚µ‚ؤژںŒ³•ھ‘S‚ؤ‚جƒ°‚ًژو‚éپx‚ئŒ¾‚¤‚à‚ج‚إ‚·پB
پ@ƒچپ[ƒŒƒ“ƒc‹t•دٹ·ژ®‚حŒWگ”‚k‚ج‹tچs—ٌ‚ًژg‚¢پA
پ@پ@
‚ئڈ‘‚ژ–‚ھڈo—ˆ‚ـ‚·پB
ڈ®پAƒچپ[ƒŒƒ“ƒcŒWگ”‚ج‹tچs—ٌٹضŒW‚ًژQچl‚ـ‚إ‚ة
پ@پ@
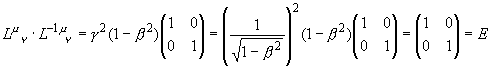
‚d‚حچs—ٌ•—‚ةŒ¾‚¦‚خ’Pˆتچs—ٌ‚إ‚·پB
پ@گiچs•ûŒü‚ةگ‚’¼‚بچہ•Wژ²‚ً’ا‰ء‚µ‚ؤپAƒچپ[ƒŒƒ“ƒc•دٹ·‚جŒWگ”‚ً‚SژںŒ³•ھ‘S‚ؤ•\‚·‚ئپA
پ@پ@
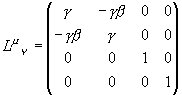
‚ئ‚ب‚è‚ـ‚·پB
‚PپD‚WپD‚Rپ@•s•د—ت‚ئ‹——£
پ@ژں‚ةپA‚±‚جƒ~ƒ“ƒRƒtƒXƒLپ[ژ‹َ‚ة‚آ‚¢‚ؤچl‚¦‚ؤ‚ف‚ـ‚µ‚ه‚¤پB
پ@ƒjƒ…پ[ƒgƒ“‚حپA—حٹw‚ًژ؟“_‚جˆت’u‚ئژٹش‚جٹضگ”‚إ’è‹`‚µ‚ـ‚µ‚½پB’تڈيپAژ؟“_‚جˆت’u‚حپ@پi‚ک‚P,‚ک‚Q,‚ک‚Rپjپ@‚ب‚ا3ژںŒ³‚ج’¼چs’¼گüچہ•WپiƒfƒJƒ‹ƒgچہ•Wپj‚إ•\‚µپAژٹش‚ح‘S‰F’ˆ‚جژ؟“_‹¤’تپi“ءژê‘ٹ‘خگ«—ک_‚إ‚حٹµگ«Œn‚ةŒإ—L‚جژٹش‚ًچl‚¦‚ـ‚µ‚½‚ھپj‚إ‚ ‚é‚ئچl‚¦پA‚PŒآ‚ج•دگ”پ@‚”پ@‚ب‚ا‚إ•\‚µ‚ـ‚·پB
پ@ژ؟“_‚ح‚RژںŒ³‚جƒfƒJƒ‹ƒgچہ•W‚إ•\Œ»ڈo—ˆ‚éˆبڈمپAƒ†پ[ƒNƒٹƒbƒh‹َٹش‚ة‘¶چف‚·‚é‚ئ‚³‚ê‚ـ‚µ‚½پB‚آ‚ـ‚肱‚ج•¨—‹َٹشپE‘S‰F’ˆ‚حƒ†پ[ƒNƒٹƒbƒh‹َٹش‚ة‚ح‚كچ‚ـ‚ê‚ؤ‚¨‚èپA‘S‰F’ˆ‹¤’ت‚جژٹش‚ةچ‡‚ي‚¹‚ؤپA•¨—Œ»ڈغ‚ھ‹N‚«‚ؤ‚¢‚é‚ئچl‚¦‚é‚ي‚¯‚إ‚·پB
‚à‚؟‚ë‚ٌ•¨—Œ»ڈغ‚ً‹Lڈq‚·‚éڈم‚إپA‘¼‚ج‹بگüچہ•WŒnپA—ل‚¦‚خ‘ب‰~چہ•W‚â‹…چہ•W‚ب‚ا‚ھ“sچ‡‚ھ—ا‚¢ڈêچ‡‚حپA‹Z–@‚ئ‚µ‚ؤƒfƒJƒ‹ƒgچہ•WˆبٹO‚ً—p‚¢‚邱‚ئ‚ًچs‚¤‚ي‚¯‚إ‚·‚ھپB
پ@پwƒ†پ[ƒNƒٹƒbƒh‹َٹش‚âژٹش‚ح’N‚ھچى‚ء‚½‚ج‚إ‚µ‚ه‚¤‚©پHپ@گ_—l‚إ‚·پBپ@‚¢‚â‚¢‚âچإڈ‰‚©‚çچف‚ء‚½‚ٌ‚إ‚µ‚ه‚¤پBپ@‰]پX‚©‚ٌ‚ت‚ٌپx‚ئŒ¾‚¤‚س‚¤‚ةپAپw•¨—ˆب‘O‚جژ©–¾‚بٹT”O‚إ‚ ‚èپA‚ ‚¦‚ؤŒ¾‚¦‚خگ_ٹw‚â“Nٹw‚ج”حلe‚إ‚ ‚éپx‚ئپAƒjƒ…پ[ƒgƒ“‚à“V‰؛‚è“I‚ةژٹشپA‹َٹش‚جٹT”O‚ًژَ‚¯“ü‚ê‚ؤ‚¢‚½—l‚إ‚·پB
‚±‚جپwƒ†پ[ƒNƒٹƒbƒh‹َٹش‚إ‰F’ˆ‚حڈo—ˆ‚ؤ‚¢‚éپx‚ئ‚¢‚¤”‘z‚حپAƒjƒ…پ[ƒgƒ“‚ب‚炸‚ئ‚àپA‚²‚‚²‚ژ©‘R‚ب‚à‚ج‚إپA’†ٹwچZ‚جگ”ٹw‚ب‚ا‚إچہ•W‚âƒOƒ‰ƒt‚جژِ‹ئ‚ًژَ‚¯‚é‚ئپA‚ ‚ء‚ئŒ¾‚¤ٹش‚ة‚±‚جگ¢‚ج’†‚حƒ†پ[ƒNƒٹƒbƒh‹َٹش‚¾‚ئŒه‚ء‚ؤ‚µ‚ـ‚¢‚ـ‚·پB’†ٹwچZ‚جگوگ¶‚حپA‚±‚جگ¢‚ج’†‚حƒ†پ[ƒNƒٹƒbƒh‹َٹش‚إ‚«‚ؤ‚¢‚é‚ب‚ا‚ئ‚حپA‹³‚¦‚ؤ‚¢‚ب‚¢‚ح‚¸‚ب‚ج‚إ‚·‚ھپB
ˆبچ~پAژ„‚½‚؟‚حƒ†پ[ƒNƒٹƒbƒh‹َٹش‚ئ‚¢‚¤–¼‘O‚ح–Y‚ê‚ؤ‚àپA‚±‚جٹT”O‚ج’†‚إ‘S‚ؤ‚ًچl‚¦‚é‚و‚¤‚ة‚ب‚è‚ـ‚·پB
‚µ‚©‚µپA‘ٹ‘خگ«—ک_‚â—تژq—حٹw‚ً’m‚邤‚؟‚ةپA‚±‚ج•¨—‹َٹش‚ة‘خ‚·‚éٹT”O‚حپAŒ»ژہگ¶ٹˆڈم‚ج•ض–@‚إ‚µ‚©‚ب‚©‚ء‚½‚±‚ئ‚ةپA‹C•t‚©‚³‚ê‚ـ‚·پB
‚»‚ê‚إ‚حچہ•W•دٹ·‚ً‚à‚ئ‚ةپAƒ†پ[ƒNƒٹƒbƒh‹َٹش‚جچ\‘¢‚©‚ç’T‚ء‚ؤ‚ف‚ـ‚µ‚ه‚¤پBپ@‹َٹش‚جڈd—v‚ب—v‘f‚ئ‚µ‚ؤپh‹——£پh‚ح‚ا‚ج‚و‚¤‚ة’è‹`‚³‚ê‚ؤ‚¢‚é‚ج‚إ‚µ‚ه‚¤‚©پB
‚ـ‚¸‚حپA‚QژںŒ³‹َٹش‚جƒfƒJƒ‹ƒgچہ•WX‚إچl‚¦‚ـ‚·پBپ@“ٌ“_ٹش‚ج”÷ڈ¬‹——£‚ًƒ¢‚“‚ئ‚·‚é‚ئپA‹——£‚ج“ٌڈوپA
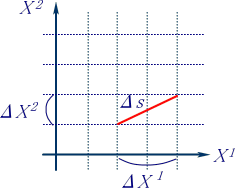
ژہچغ‚ةƒپƒ‚ƒٹ‚ً“ا‚ٌ‚إŒ©‚ـ‚µ‚ه‚¤پB
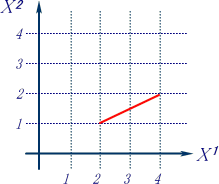
‚±‚جگش‚¢گü‚ً“¯‚¶ƒپƒ‚ƒٹ‚ًگU‚ء‚½•ت‚جچہ•WŒn‚ک(—خ)‚إ“ا‚ٌ‚إŒ©‚ـ‚µ‚ه‚¤پB چ،‰ٌپAچہ•W‚ک‚ح‰؛‚ة‚QپA‰E‚P‚ة‚¸‚炵‚½ˆت’u‚ئ‚µ‚ـ‚·پB
پ@‚â‚ح‚è‹——£‚حپم‚T‚إ‚·پBپ@“–‚½‚è‘O‚إ‚·‚©پHپ@‚»‚¤‚حŒ¾‚ء‚ؤ‚à—خ‚جچہ•W‚ًچى‚é‚ئ‚«‚ةپAگ³ٹm‚ةگآ‚جŒ³‚جچہ•W‚ًƒRƒsپ[‚µپAڈمژè‚‚¸‚炵‚ؤڈd‚ث‚ب‚¯‚ê‚خ‚ب‚è‚ـ‚¹‚ٌ‚إ‚µ‚½پBپ@Œ‹چ\ژèٹش‚ب‚ٌ‚إ‚·پB
پ@چہ•W‚ً‚¢‚؟‚¢‚؟–ع‚إ“ا‚فڈم‚°‚é‚ج‚ح‘ه•د‚إ‚·پB•دٹ·ژ®‚ًژg‚¢‚ـ‚µ‚ه‚¤پBپ@—خ‚ج‚کچہ•W‚©‚çگآ‚¢Œ³‚جXچہ•W‚ض‚ج•دٹ·ژ®پiŒµ–§‚ة‚حپAŒ³‚جچہ•W‚ة–ك‚·‚±‚ئ‚ً‹t•دٹ·‚ئŒؤ‚رپA‹t•دٹ·ژ®‚ئ‚¢‚¤‚±‚ئ‚ب‚è‚ـ‚·پj‚حپA‰؛‚ة‚QپA‰E‚P‚ة‚¸‚炵‚½ˆت’u‚إ‚·‚©‚ç
پ@پ@پ@پ@
‚ئ‚ب‚è‚ـ‚·پBپ@گü•ھ‚ج—¼’[‚جˆت’u‚ًŒ³‚جچہ•W‚ة•دٹ·‚µ‚ؤپA‹——£‚ً‹پ‚ك‚ؤ‚à“¯‚¶‚ة‚ب‚邱‚ئ‚حپAٹm‚©‚ك‚é‚ـ‚إ‚à–³‚–¾”’‚إ‚·‚ثپB
پ@‚ئ‚±‚ë‚إپA•ت‚جچہ•WŒn‚إ“ا‚ٌ‚¾’l‚ًپAŒ³‚جچہ•WŒn‚ة“ا‚ف’¼‚·ڈêچ‡‚ج•دٹ·ژ®‚حپAˆب‰؛‚ج‚و‚¤‚ةٹضگ”‚ًژg‚ء‚ؤˆê”ت‰»پiˆê”تچہ•W•دٹ·پj‚³‚ê‚ـ‚·پBپ@ƒpƒ‰ƒپپ[ƒ^‚ح•دٹ·‘O‚جچہ•WƒZƒbƒg‚إ‚·پB
پ@پ@پ@پ@
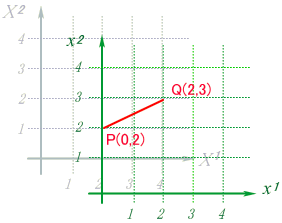
ƒCƒپپ[ƒW‚ئ‚µ‚ؤ‚حپAˆب‰؛‚جگ}‚ج—l‚ة‚ک‚PپC‚ک‚Q‚ً“ٌژںŒ³‚ج•دگ”‚ئ‚µ‚ؤژOژںŒ³–ع‚ةX‚PپCX‚Q‚جٹضگ”‚ھ‚»‚ꂼ‚ê’è‹`‚³‚ê‚ؤ‚¢‚é‚ئ‚¢‚ء‚½ڈٹ‚إ‚µ‚ه‚¤‚©پB
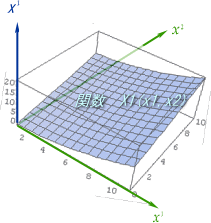 پ@پ@پ@پ@
پ@پ@پ@پ@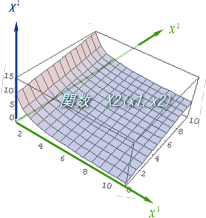
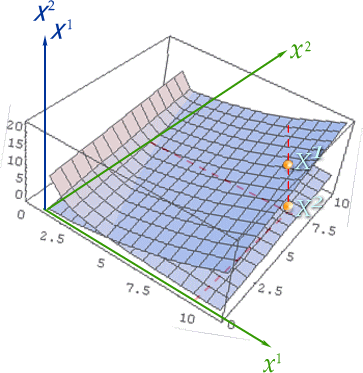 پ@پ@پ@پ@
پ@پ@پ@پ@ ‚à‚؟‚ë‚ٌ‚ک‚PپC‚ک‚Q‚جچہ•W‚ًگ}‚ج—l‚ة’¼گü’¼چsچہ•WپiƒfƒJƒ‹ƒgچہ•Wپj‚ة•`‚¢‚½‚±‚ئ‚حپA’P‚ةƒCƒپپ[ƒW‚ً‚آ‚©‚فˆہ‚‚·‚邽‚ك‚ج•ض‹Xڈم‚ج‚±‚ئ‚إ‚·پBپ@“ءژê‘ٹ‘خگ«—ک_‚إ‚جˆع“®Œn‚rپf‚ةڈZ‚ٌ‚إ‚¢‚éگl‚½‚؟‚حپAگأژ~Œn‚©‚猩‚ؤپA‚ ‚ٌ‚ب‚ةچہ•Wژ²‚ھ‚ذ‚µ‚ل‚°‚ؤ‚µ‚ـ‚ء‚ؤ‚¢‚ؤ‚àپAژ©•ھ‚جŒn‚حƒfƒJƒ‹ƒgŒn‚ئژv‚ء‚ؤ‚¢‚½‚ي‚¯‚إ‚·‚µپB
پ@ژں‚ةچہ•W‚ً‰ٌ“]‚³‚¹‚ؤŒ©‚ـ‚µ‚ه‚¤پB
پ@گ}‚ج—l‚ةپA–ٌ‚Q‚Vپ‹‰ٌ“]‚³‚¹‚é‚ئ‚ز‚ء‚½‚èڈd‚ب‚è‚ـ‚·پB
ƒپƒ‚ƒٹ‚ً“ا‚ٌ‚إŒ©‚ـ‚µ‚ه‚¤پBگü•ھ‚جچ¶‰؛’[‚ج‚ک‚Pژ²‚ح‚QپD‚Q‚R‚U‚®‚ç‚¢‚ـ‚إ“ا‚فژو‚ê‚ـ‚·‚©پHپ@ƒپƒ‚ƒٹ‚ھ‘e‚·‚¬‚إ–³—‚إ‚·‚ثپBپ@Œ³‚جچہ•Wڈم‚إژOٹpŒ`‚جژخ•س‚ج’·‚³‚ئ‚µ‚ؤŒ©‚ب‚¹‚خپAگ³ٹm‚ةپم‚TپA‚¢‚ي‚ن‚éپu•xژmژRک[پEپEپEپv‚¾‚ئٹm”F‚إ‚«‚ـ‚·پBپ@“¯—l‚ة‰Eڈم’[‚ح‚Qپم‚TپA–ٌ‚SپD‚S‚V‚Q‚ئ‚¢‚ء‚½‚ئ‚±‚ë‚إ‚µ‚ه‚¤‚©پBپ@‚à‚؟‚ë‚ٌ‚ک‚Qژ²‚ج•û‚ح—¼’[‹¤‚O‚إ‚·پB
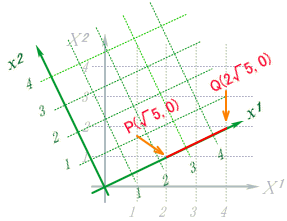
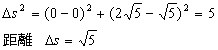
‚±‚جڈêچ‡‚جŒ³‚جچہ•W‚ة–ك‚·•دٹ·ژ®‚ح‚ا‚¤‚ب‚é‚ج‚إ‚µ‚ه‚¤‚©پHپ@چ¶‰ٌ‚è‚ة
پ@پ@پ@پ@
ژژ‚µ‚ة‚±‚ê‚ًژg‚ء‚ؤپA‚کچہ•Wڈم‚ج‰Eڈم’[‚جƒپƒ‚ƒٹ‚ًپAŒ³‚جXچہ•W‚ة‹t•دٹ·‚µ‚ؤ‚ف‚ـ‚µ‚ه‚¤پB
پ@پ@پ@پ@
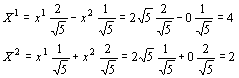
Xچہ•W‚جƒپƒ‚ƒٹپi‚SپC‚Qپj‚ھ‹پ‚ـ‚è‚ـ‚·پB“¯—l‚ةچ¶‰؛’[‚جƒپƒ‚ƒٹ‚حپi‚QپC‚Pپj‚ئ‚ب‚èپA‚â‚ح‚è‹——£‚حپم‚T‚ئ‚ب‚è‚ـ‚·پB
پ@‚±‚ج‚و‚¤‚ةپAچہ•W‚ھ•د‚é‚ئ“–‘Rƒپƒ‚ƒٹ‚ج“ا‚ف‚ح•د‚ي‚ء‚ؤ‚«‚ـ‚·‚ھپA‹——£‚ح•s•د‚إ‚·پBپ@“–‚½‚è‘O‚¾پI‚ئŒ¾‚ي‚ê‚»‚¤‚إ‚·‚ھپA‚±‚ج•s•د‚ئ‚¢‚¤ژ–‚ھŒمپXڈd—v‚بˆس–،‚ًژ‚آ‚و‚¤‚ة‚ب‚è‚ـ‚·پB
‚PپD‚WپD‚Tپ@Œv—ت
پ@‘±‚¢‚ؤچہ•Wژ²‚ھڈk‚ق‚ئ‚ا‚¤‚ب‚é‚ج‚إ‚µ‚ه‚©پBˆب‰؛‚ج—l‚ةƒپƒ‚ƒٹ‚ھچׂ©‚‚ب‚è‚ـ‚·پB‚±‚جچہ•W‚إگü•ھ‚ً‘ھ‚é‚ئQپi‚SپC‚SپjپAPپi‚QپC‚Qپj‚ب‚ج‚إ‹——£‚ح‚Qپم‚Q‚ئ‘ه‚«‚‚ب‚ء‚ؤ‚µ‚ـ‚¢‚ـ‚·پB
پ@پw‚±‚ٌ‚بچہ•WپAژg‚¦‚ـ‚¹‚ٌپIپx‚ئŒ¾‚ي‚ê‚»‚¤‚إ‚·پBپ@‚ئ‚±‚ë‚ھ‚ک2چہ•W‚ھڈk‚ٌ‚إ‚¢‚邾‚¯‚ب‚ج‚إپA‚ک2ژ²‚ج“ا‚ف‚ً
پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پw‚P/‚Q‚ة•âگ³پx
‚·‚邾‚¯‚إ‹——£‚ح‘ھ‚ê‚ـ‚·پBپ@“ء•ت‚جژèٹش‚ھ‘‚¦‚é•ھ‚¯‚إ‚ح‚ ‚è‚ـ‚¹‚ٌپB
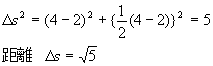
پ@پ@پ@پ@
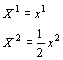 پ@
پ@Œ³‚جچہ•W‚ة•دٹ·‚µ‚ؤ‹——£‚ًٹm”F‚µ‚ؤ‚ف‚ـ‚µ‚ه‚¤پB
پ@پ@پ@پ@
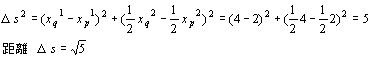
گLڈk‚جڈêچ‡‚حپA‚¸‚炵‚½‚èپA‰ٌ“]‚³‚¹‚½ڈêچ‡‚ئ‚‚ç‚×پw•âگ³پx‚ھ•K—v‚ئ‚ب‚è‚ـ‚µ‚½پB
پ@ژں‚حچہ•W‚ًŒX‚¯‚ؤ‚ف‚ـ‚µ‚ه‚¤پB
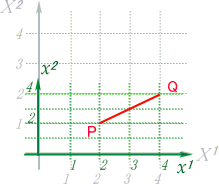
گ}‚إ‚ک2چہ•W‚جŒX‚«‚ح‚S‚Tپ‹‚إ‚·پB
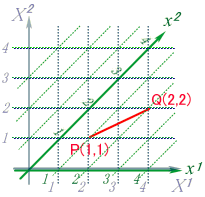
‚د‚ء‚ئŒ©پAپw‚ک1ژ²‚ً2”{‚ة•âگ³پx‚ئŒ¾‚¢‚½‚¢ڈٹ‚إ‚µ‚ه‚¤‚©پB
S2پپ(1¥2)2پ{‚P2پپ5 ‚ئ‚ب‚ء‚ؤپAŒ©‚é‚©‚ç‚ةگ³‚µ‚»‚¤‚إ‚·پB
‚ئ‚±‚ë‚ھژں‚جگ}‚إ‚ح‚ا‚¤‚إ‚µ‚ه‚¤‚©پH
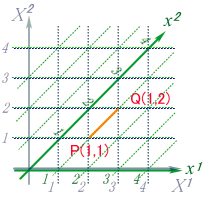
S2پپ(0¥2)2پ{12پپ1‚ئ‚ب‚ء‚ؤ‚µ‚ـ‚¢‚ـ‚·پB‚à‚؟‚ë‚ٌŒ³‚جXچہ•W‚إ‚حS2پپ2‚ة‚ب‚è‚ـ‚·‚©‚çپA‚±‚ج•âگ³•û–@‚إ‚ح‚¾‚ك‚إ‚·‚ثپB
پ@گ³‚µ‚¢•âگ³•û–@‚ً’T‚ء‚ؤ‚ف‚ـ‚µ‚ه‚¤پB
‚±‚جڈêچ‡‚ج‹t•دٹ·ژ®‚ح‚ک2چہ•W‚جŒX‚«‚ًƒئ‚ئ‚·‚é‚ئ
پ@پ@
tanƒئ‚ح’èگ”‚إ‚·پBپ@‚S‚Tپ‹‚جڈêچ‡‚ح‚P‚ب‚ج‚إ‚·‚ھ‚پ‚ئ‚µ‚ـ‚µ‚ه‚¤پB
پ@پ@
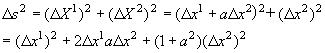
a=1‚ئ’u‚¢‚ؤپA‘پ‘¬ŒںژZ‚µ‚ؤ‚ف‚ـ‚µ‚ه‚¤پB
‡™x1=0, ‡™x2=1‚إ‚·‚©‚çپA
پ@پ@‡™S2پپ02پ{0پ{2¥12پپ2
‚ئ‚ب‚èپAچ‡‚ء‚ؤ‚¢‚ـ‚·پB
”O‚ج‚½‚كپA‚»‚ج‘O‚جƒPپ[ƒXپA‡™x1=1, ‡™x2=1‚جڈêچ‡‚àS2پپ5‚ة‚ب‚é‚©پAٹm”F‚µ‚ؤ‚ف‚ـ‚µ‚ه‚¤پB
پ@پ@‡™S2پپ12پ{2+2¥12پپ5
‚ئ‚ب‚è‚ـ‚µ‚½پBپ@‚ف‚²‚ئپAچ‡ٹi‚إ‚·پB
‚ئ‚±‚ë‚إ
پ@پ@
‚ئ‚¢‚¤ژ®‚ح
پ@پ@
پ@پ@‚½‚¾‚µپA
‚ئ‚¢‚¤‚و‚¤‚ةپAگ®—ڈo—ˆ‚ـ‚·پB
‚³‚ç‚ة‡™‚ک‚ًƒxƒNƒgƒ‹پA’èگ”•”‚‡‚ًچs—ٌ‚ج‚»‚ꂼ‚ê—v‘f‚ئŒ©‚ب‚·‚ئپA
پ@پ@
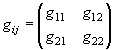
‚ئ•\‚¹‚ـ‚·پB
‚‡‚حŒv—تپiƒپƒgƒٹƒbƒNپjƒeƒ“ƒ\ƒ‹‚ ‚é‚¢‚حٹî–{ƒeƒ“ƒ\ƒ‹‚ئŒؤ‚خ‚êپA‹َٹش‚ج‹——£‚ً’è‹`‚·‚éچs—ٌ‚إ‚·پBˆê”ت‘ٹ‘خگ«—ک_‚ً—‰ً‚·‚éڈم‚إڈd—v‚بٹT”O‚إ‚ ‚èپAچ،Œم‚µ‚خ‚µ‚خڈo‚ؤ‚«‚ـ‚·پB
چ،‰ٌ‚ج—ل‚إ‚¢‚¤‚ئپA
پ@پ@پ@پwx2چہ•W‚ھƒئ=‚S‚Tپ‹ŒX‚¢‚½چہ•W‚إ•\‚³‚ê‚é2ژںŒ³‹َٹش‚جŒv—ت‚ح
پ@پ@پ@پ@پ@پ@پ@پ@
پ@پ@پ@‚إ‚·پx
‚ئ‚¢‚¤‚و‚¤‚بژg‚ي‚ê•û‚ة‚ب‚è‚ـ‚·پB
‚³‚ç‚ةˆê”ت‘ٹ‘خگ«—ک_‚إ‚µ‚خ‚µ‚خپi‚ئŒ¾‚¤‚و‚è‚حپA‚µ‚ه‚ء‚؟‚م‚¤پjŒ»‚ي‚ê‚é•\‹L–@‚ئ‚µ‚ؤپA
پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@
‚ً
پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@
‚ئڈب—ھ‚µ‚ؤ•\‹L‚µ‚ـ‚·پB‚±‚ê‚حƒAƒCƒ“ƒVƒ…ƒ^ƒCƒ“‚جپwڈk–ٌ‚ج‹K‘¥پx‚ئ‚¢‚¤‚à‚ج‚إ‚·پB
پwچ€‚ج’†‚إƒxƒNƒgƒ‹‚ب‚èپAچs—ٌ‚ج“¯‚¶“Yژڑ‚ھڈم‰؛‚ةڈo‚ؤ‚«‚½‚çپAگدکa‚ًژو‚éپx‚ئ‚¢‚¤‚à‚ج‚إ‚·پBگڈ•ھپA‚·‚ء‚«‚茩‚¦‚ـ‚·‚ثپB
پ@پwŒv—ت‚ح‚¢‚¢‚ئ‚µ‚ؤپA‚ي‚´‚ي‚´‚±‚ٌ‚بپA‚ض‚ٌ‚ؤ‚±‚è‚ٌ‚بچہ•W‚إŒv‚ء‚ؤ‰½‚ھ‚¤‚ꂵ‚¢‚ج‚©پHپx‚ئŒ¾‚ي‚ê‚»‚¤‚إ‚·پBپ@‚»‚ج’ت‚è‚إپA‚±‚جڈêچ‡‚ح“ء‚ة‚¤‚ꂵ‚‚à—L‚è‚ـ‚¹‚ٌپBپ@•¨—“I‚بˆس–،‚ح“ء‚ة—L‚è‚ـ‚¹‚ٌپBپ@چ،ŒمپAژ‹َچہ•W‚ًˆµ‚¤ڈم‚إ‚جگ”ٹwƒgƒŒپ[ƒjƒ“ƒO‚ئژv‚ء‚ؤ‚‚¾‚³‚¢پB
پ@‚ئ‚±‚ë‚إپAچ،‚ـ‚إ‚ةڈo‚ؤ‚«‚½‹t•دٹ·ژ®‚ً‚à‚¤ˆê“x•ہ‚ׂؤŒ©‚ؤ‚ف‚ـ‚µ‚ه‚¤پB
| ‡@چہ•W‚ج•½چsˆع“® پi‚¸‚炵پj |
‡Aچہ•W‚ج‰ٌ“] | ‡Bچہ•W‚جگLڈk | ‡Bچہ•W‚جŒX‚¯ |
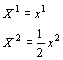 |
ژہ‚حپA‚±‚ê‚ç‚جژ®‚حˆب‰؛‚ج—l‚ةچs—ٌ‚جژ®‚إ•\Œ»‚إ‚«‚ـ‚·پB
پ@پ@پ@پ@
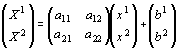
ژہچغ‚ة“–‚ؤ‚ح‚ك‚ؤŒ©‚ـ‚µ‚ه‚¤پB
| ‡@چہ•W‚ج•½چsˆع“® پi‚¸‚炵پj |
‡Bچہ•W‚ج‰ٌ“] |
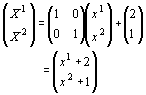 |
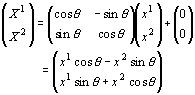 |
| ‡Bچہ•W‚جگLڈk | ‡Cچہ•W‚جŒX‚¯پiژخŒًچہ•Wپj |
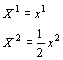 |
|
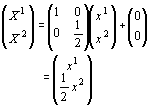 |
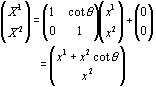 پ@ پ@ |
‚»‚ꂼ‚êڈمژè‚
پ@پ@پ@پ@
‚ئ‚¢‚¤چs—ٌ‚ج‚Pژںژ®‚جŒ`‚ة”[‚ـ‚è‚ـ‚·پB
پ@‚±‚ج‚و‚¤‚بŒ`‚ة•دٹ·ژ®‚ًڈ‘‚«•\‚¹‚é•دٹ·‚ًƒAƒtƒ@ƒCƒ“•دٹ·‚ئŒؤ‚ر‚ـ‚·پBپ@“ْڈيپA–ع‚ة‰f‚镨‚جŒ`‚حژ‹“_‚ة‚و‚è•دŒ`‚µ‚ـ‚·پBپ@‚±‚جŒ©‚½–ع‚ج•دŒ`‚حپAƒAƒtƒ@ƒCƒ“•دٹ·‚جˆê—ل‚إ‚·پB
پ@گو‚ظ‚اپA‚±‚ê“™‚جچہ•W•دٹ·‚ة•¨—“I‚بˆس–،‚ح–³‚¢‚ئŒ¾‚¢‚ـ‚µ‚½‚ھپAژہ—p–ت‚إ‚ح‚¢‚ë‚¢‚ë‚ئˆس–،‚ھ‚ ‚è‚ـ‚·پBپ@—ل‚¦‚خپAƒRƒ“ƒsƒ…پ[ƒ^ƒOƒ‰ƒtƒBƒbƒNƒX‚ب‚ا‚إ‚حƒAƒtƒ@ƒCƒ“•دٹ·‚ً—ک—p‚µ‚ؤپA—§‘ج‰و‘œ‚ًŒvژZ‚µ‚ؤ‚¢‚ـ‚·پBپ@‚¢‚ي‚ن‚é‚RD‚جCGƒQپ[ƒ€‚ب‚ا‚ھگg‹ك‚ب‰—p—ل‚إ‚µ‚ه‚¤‚©پBپ@“¹—‚إ‚±‚ê‚ç‚ج•دٹ·—ل‚حپAŒ©ٹo‚¦‚ھ—L‚ء‚½پH‚ي‚¯‚إ‚·‚ثپB
ژ‹“_‚ھ—£‚ê‚ؤپA•¨‚ج‘ه‚«‚³‚ھڈ¬‚³‚Œ©‚¦‚½‚ئ‚µ‚ؤ‚àپA‚»‚ج•¨‚ج’·‚³‚ھڈk‚ٌ‚¾‚ي‚¯‚إ‚ح—L‚è‚ـ‚¹‚ٌپB
‚»‚ٌ‚بڈيژ¯“I‚بژ–‚ً‚¢‚؟‚¢‚؟‹’²‚·‚é‚ب‚ئŒ¾‚ي‚ê‚»‚¤‚إ‚·پBپ@‚µ‚©‚µڈيژ¯“I‚ة‚حژ—‚½‚èٹٌ‚ء‚½‚è‚جپA‚·‚êˆل‚¢‚ب‚ھ‚ç’‚ك‚½ڈêچ‡‚ج•دٹ·‚ھپAƒچپ[ƒŒƒ“ƒc•دٹ·‚¾‚ء‚½‚ي‚¯‚إ‚·پBپ@‚»‚µ‚ؤپA‚»‚جƒچپ[ƒŒƒ“ƒc•دٹ·‚إ‚حپA‚ـ‚³‚ة’·‚³‚ھڈk‚ٌ‚إ‚µ‚ـ‚ء‚ؤ‚¢‚ـ‚µ‚½پB
ˆê”ت‚ة•دٹ·ژ®‚حƒAƒtƒ@ƒCƒ“•دٹ·‚ج—l‚ةگüŒ`‚ئ‚حŒہ‚è‚ـ‚¹‚ٌپBپ@ƒXƒvپ[ƒ“‚جکc‚ٌ‚¾ژت‘œ‚جڈêچ‡‚ج—l‚ةپA‚ا‚¤چl‚¦‚ؤ‚à‹بگüچہ•W‚ة•دٹ·‚¹‚´‚é‚ً“¾‚ب‚‚ب‚éڈêچ‡‚ھڈo‚ؤ‚‚é‚إ‚µ‚ه‚¤پBپ@•دٹ·ژ®‚حکA‘±‚إ‚©‚آپAŒف‚¢‚ةˆê‰؟پi•دٹ·گو‚ھ‚Q“_ˆبڈم‚ة‘خ‰‚µ‚ب‚¢پj‚إ‚ ‚肳‚¦‚·‚ê‚خگ¬‚è—§‚؟‚ـ‚·پBپ@‚»‚جڈêچ‡‚ج‚کچہ•W‚ح‹بگüچہ•WŒn‚ئ‚ب‚è‚ـ‚·پB
ˆê”تچہ•W•دٹ·‚ج—ل‚ئ‚µ‚ؤ‹ةچہ•W‚ض‚ج•دٹ·‚ًچl‚¦‚ـ‚µ‚ه‚¤پB
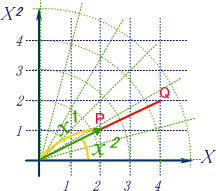
‚±‚جڈêچ‡‚ج•دٹ·ژ®‚ح
پ@پ@پ@پ@
‚إ‚·پB ‹ةچہ•W‚ک‚إ‚ج“ا‚ف‚ح
پ@پ@پ@پ@
‚ئ‚ب‚è‚ـ‚·پBپ@‹ةچہ•W‚ک‚إŒv‚ء‚½‹——£‚ح
پ@پ@پ@پ@
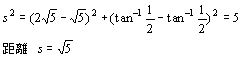
‚â‚ح‚è‹——£‚حˆê’v‚µ‚ـ‚·پBپ@پwٹp“x•ûŒü‚جگ¬•ھ‚ک‚Q‚ھڈء‚¦‚ؤ‚¢‚é‚©‚çپA‚¾‚ـ‚³‚ꂽ—l‚ب‹C•ھپIپx‚إ‚·‚ثپB
پ@‚±‚ج‹ةچہ•W‚à’¼چsچہ•W‚جˆêژي‚إپA‹بگü’¼چsچہ•W‚ئ‚¢‚¤‚à‚ج‚جˆê‚آ‚إ‚·پBپ@‚µ‚©‚µ‹ة‚©‚牓‚´‚©‚é‚ظ‚اپAٹp“x•ûŒü‚جگ¬•ھ‚ک2‚حƒپƒ‚ƒٹ•‚ھگL‚ر‚ؤپA’·‚³‚ج’l‚ھڈ¬‚³‚‚ب‚ء‚ؤ‚µ‚ـ‚¢‚ـ‚·پBپ@‚آ‚ـ‚èپAڈêڈٹ‚ة‚و‚ء‚ؤƒپƒ‚ƒٹ‚ھˆل‚¤‚ج‚إپA”Cˆس‚ج‚Q“_ٹش‚ج‹——£‚ًŒv‚é‚ج‚ح“‚‚ب‚è‚ـ‚·پB
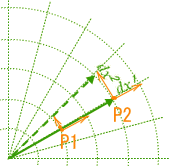
‚±‚ج‚و‚¤‚بڈêڈٹ‚ة‚و‚èƒپƒ‚ƒٹ‚ج‹ذ‚ھ•د‚ي‚ء‚ؤ‚‚éڈêچ‡‚ج‹——£‚ج‘ھ‚è•û‚ً’T‚ء‚ؤŒ©‚ـ‚µ‚ه‚¤پB
پ@‚کچہ•Wڈم‚ج”Cˆس‚ج“_‚o‚ج‹ك–T‚إ”÷ڈ¬‹——£‚ً‚„‚“چl‚¦‚ـ‚·پBپ@پwگو‚ظ‚ا‚جگà–¾‚إپA‚oپ|‚pٹش‚جƒ¢‚“‚à”÷ڈ¬‹——£‚إ‚ح‚ب‚©‚ء‚½‚ج‚©پHپx‚ئ‚¨‚ء‚µ‚ل‚ç‚ê‚»‚¤‚إ‚·پB
‚»‚¤‚إ‚·پBپ@‚»‚ج’ت‚è‚إ‚·پBپ@گà–¾‚ج“sچ‡ڈم‚µ‚ء‚©‚èچہ•W‚ًچہ•Wژ²‚جƒپƒ‚ƒٹ‚إ“ا‚ٌ‚إ‚¨‚è‚ـ‚µ‚½پBپ@‚آ‚ـ‚è”÷ڈ¬‹——£‚ئ‚¢‚¤‚س‚ꂱ‚ف‚ة‚à‚©‚©‚ي‚炸پA–ع‚ةŒ©‚¦‚éپH‘ه‚«‚³‚جƒ¢‚“‚¾‚ء‚½‚ي‚¯‚إ‚·پB
‚µ‚©‚µپAچ،Œم‹بگüچہ•W‚ًˆµ‚¤ڈم‚إ‚حپAچہ•W‚ج‹ب‚ھ‚è‹ïچ‡‚ھ–³ژ‹‚إ‚«‚é‚ظ‚ا‚ج”÷ڈ¬‚³‚ھ•K—v‚ئ‚ب‚è‚ـ‚·پBپ@‚»‚ج‚½‚كچ،‰ٌ‚ج‚„‚“‚ح”÷گد•ھ‚إڈo‚ؤ‚«‚½پA‚¢‚ي‚ن‚é‹ةŒہ“I‚ةڈ¬‚³‚¢–³Œہڈ¬‹——£‚ج‚„‚“‚إ‚·پB
‚ ‚ـ‚è‚ة‚àڈ¬‚³‚¢‚ج‚إپA‚„‚“‚ًŒp‚¬‘«‚µ‚ؤ‹بگü‚ًچ\گ¬‚·‚邱‚ھ‰آ”\‚ئ‚ب‚é‚و‚¤‚بپA‹ةڈ¬’¼گü‚إ‚·پBپ@‚±‚ê‚ًپwگü‘fپx‚ئŒؤ‚ر‚ـ‚·پB
پ@‘O’u‚«‚ھ’·‚‚ب‚è‚ـ‚µ‚½‚ھپA‚کچہ•Wڈم‚جگü‘f‚„‚“‚ج’·‚³‚ً‚ً‹پ‚ك‚ؤ‚ف‚ـ‚µ‚ه‚¤پB
‹بگüچہ•WŒn‚إ‚ ‚ء‚ؤ‚àپA‚o“_‹ك–T‚إ‚حچہ•W‚ح’¼گü‚ئ‚ف‚ب‚¹‚é‚ج‚إپAگü‘f‚ة‘خ‰‚·‚é‚کچہ•Wڈم‚ج”÷ڈ¬‹——£‚ئپAXچہ•Wڈم‚ج”÷ڈ¬‹——£‚ئ‚ح“™‚µ‚‚ب‚è‚ـ‚·پBپ@‚و‚ء‚ؤپA‚ـ‚¸‚حXچہ•Wپi’¼چsچہ•WŒnپj‚إ‚ج”÷ڈ¬‹——£‚ً‹پ‚ك‚ـ‚·پB
ƒsƒ^ƒSƒ‰ƒX‚ج’è—‚ًژg‚ء‚ؤ
پ@پ@پ@
‚ئ’u‚«‚ـ‚·پB
‚³‚ç‚ة
پ@پ@پ@پ@پ@پ@پ@پ@پ@
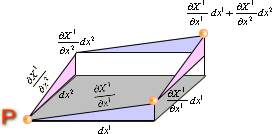
پ@پ@
پ@پ@
‚و‚ء‚ؤ
پ@
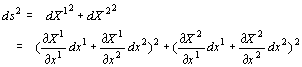
“WٹJ‚µ‚ؤ
پ@
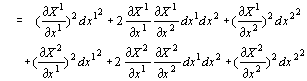
‚„‚ک‚جچ€‚إگ®—‚µ’¼‚·‚ئ
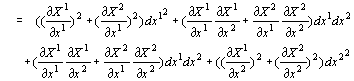
پ@
‚½‚¾‚µ
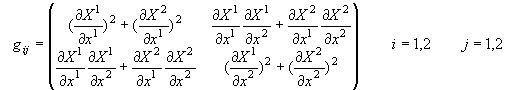
‚³‚ç‚ةƒAƒCƒ“ƒVƒ…ƒ^ƒCƒ“‚جڈk–ٌ‚ج‹K‘¥‚ًژg‚ء‚ؤ
پ@
پ@پ@پ@پ@پ@پ@پ@پEپEپEپiƒAƒCƒ“ƒVƒ…ƒ^ƒCƒ“‚جڈk–ٌ‚ج‹K‘¥‚حپA“Yژڑ‚ھڈم‰؛‚ةڈo‚éچ€‚حگدکa‚ًژو‚éپ@
پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@—لپFپ@
پ@
‚±‚±‚إ‚ج‚‡‚ح”÷ڈ¬—جˆو‚ة‚¨‚¯‚éŒv—ت‚إ‚·پB‚±‚ê‚ھ‘Sˆو‚ة“n‚ء‚ؤ•ھ‚ê‚خ‚»‚جچہ•WŒn‚إ‚ج‹——£‚ھ‹پ‚ك‚ç‚ê‚éژ–‚ة‚ب‚è‚ـ‚·پB
‘پ‘¬پA‹ةچہ•W‚جŒv—ت‚ً‹پ‚ك‚ؤ‚ف‚ـ‚µ‚ه‚¤پB
•دٹ·ژ®‚ح
پ@پ@
‚إ‚·پBپ@‚±‚ê‚ًŒv—ت‚جˆê”تژ®‚ة‘م“ü‚·‚é‚ئ
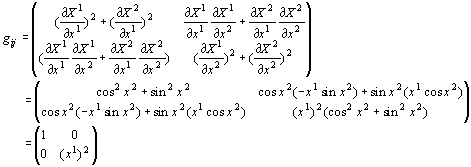
‚ھ‹پ‚ـ‚è‚ـ‚·پB
‚±‚ê‚ة‚و‚è‹——£‚ج“ٌڈو‚ح
پ@
‚ئ‹پ‚ك‚ç‚ê‚ـ‚·پB
گو‚ظ‚ا‚جƒAƒtƒ@ƒCƒ“•دٹ·‚ة‚¨‚¯‚éچہ•W‚جگLڈk—ل‚ئژ—‚ؤ‚¢‚ـ‚·پBپ@‚½‚¾‚µگLڈk‚جŒWگ”‚ھ‚ک1ژ²پA‚آ‚ـ‚è‹ة‚©‚ç‚ج‹——£‚ة”ن—ل‚·‚é“_‚ھˆظ‚ب‚ء‚ؤ‚«‚ـ‚·پBپ@
پ@‚±‚جŒv—ت‚ً‹پ‚ك‚éˆê”تژ®‚ًژg‚ء‚ؤپA‘Oڈo‚ج‚»‚ꂼ‚ê‚جچہ•W‚إ‚جŒv—ت‚ً‹پ‚ك‚ؤ‚ف‚ـ‚µ‚ه‚¤پB
‚ـ‚¸پA‚¸‚炵پi•½چsˆع“®پj‚جڈêچ‡
•دٹ·ژ®‚ح
پ@پ@پ@
Œv—ت‚ح
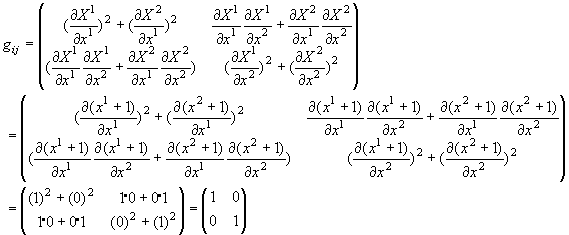
‚ئ‚ب‚è‚ـ‚·پB
‚±‚ج’²ژq‚إپA‘S•”‚ًگ®—‚µ‚ؤ‚ف‚ـ‚·پB
| چہ•W•دٹ·–¼ | ‹t•دٹ·ژ® | Œv—ت |
•دٹ·Œ³ |
ƒ†پ[ƒNƒٹƒbƒh‹َٹش [ƒfƒJƒ‹ƒgچہ•W] |
|
| ‡@چہ•W‚ج•½چsˆع“® پi‚¸‚炵پj  |
||
‡Aچہ•W‚ج‰ٌ“] |
||
‡Bچہ•W‚جگLڈk |
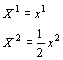 |
|
‡Cچہ•W‚جŒX‚¯ |
||
‡D‹ةچہ•W•دٹ· |
ژ‡@•½چsˆع“®‚ئ‡A‰ٌ“]‚إŒv—ت‚ح•دٹ·‘O‚ئ“¯‚¶‚إ‚ ‚邱‚ئ‚ة’چ–ع‚µ‚ؤ‚‚¾‚³‚¢پB•دٹ·‘O‚ئ•دٹ·گو‚ح“¯‚¶ƒپƒ‚ƒٹ‹ذ‚ًژ‚آ’¼گü’¼چsچہ•W‚¾‚©‚ç‚إ‚·پB‚آ‚ـ‚èچہ•WŒnژ©گg‚ة•دŒ`‚ھ–³‚¢‚½‚ك“¯‚¶Œv—ت‚ًژ‚آ‚ي‚¯‚إ‚·پB
‚±‚ê‚ً3ژںŒ³‚ةٹg’£‚µپAŒمپX‚ج‚½‚ك‚ةپA3ژںŒ³ƒ†پ[ƒNƒٹƒbƒh‹َٹش‚جŒv—ت‚ئ‚µ‚ؤ
پ@پ@پ@
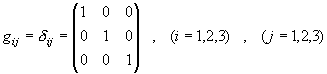
‚ئ’è‹`‚µ‚ؤ‚¨‚«‚ـ‚·پB
‚PپD‚WپD‚Uپ@‹[ƒ†پ[ƒNƒٹƒbƒh‹َٹش
ƒ~ƒ“ƒRƒtƒXƒLپ[ژ‹َگ}‚إ‚حپAژٹشژ²<‚”>‚ً–³—‚â‚è<‚ƒ‚”>‚ئ‚µپA’·‚³‚ج’Pˆت‚ًژ‚آژ²‚ة•دچX‚µ‚ـ‚µ‚½پBپ@‚»‚ج‚ ‚°‚‚ةپwگ}‚ج•\Œ»ڈم‚ح“¯‚¶‚إ‚µ‚هپx‚إ‚·پBپ@‚ب‚ٌ‚¾‚©‰ِ‚µ‚¢‚إ‚·‚ثپBپ@
ژٹش‚ئ’·‚³‚ھپA‚²‚ء‚ء‚؟‚لچ¬‚؛‚ة‚ب‚ء‚ؤ‚µ‚ـ‚ء‚½‹َٹش‚جپh‹——£پh‚ء‚ؤ‰½‚ب‚ٌ‚إ‚µ‚ه‚¤‚©پH
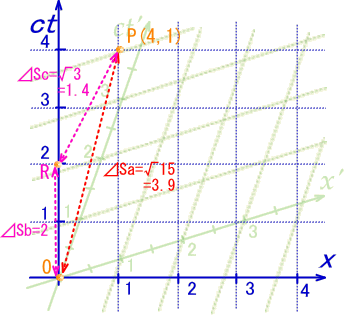
ژژ‚µ‚ةSŒn‚جچہ•WX‚إŒ´“_O‚ئPٹش‚جƒ†پ[ƒNƒٹƒbƒh‹َٹش‚إ‚ج‹——£‚ج’è‹`‚إ‡™S‚ً‘ھ‚ء‚ؤŒ©‚ـ‚µ‚ه‚¤پBƒپƒ‚ƒٹ‚ً‘هژG”c‚ة“ا‚ف‚ـ‚·پB‘½ڈ‚جŒëچ·‚ح‹C‚ة‚µ‚ب‚¢‚إ‚‚¾‚³‚¢پB
پ@ڈ®پAƒ~ƒ“ƒRƒtƒXƒLپ[ژ‹َ‚إ‚جچہ•W‚ج‚SژںŒ³•\ژ¦پi‚ƒ‚”,‚ک‚P,‚ک‚Q,‚ک‚Rپj‚ة”ُ‚¦‚ؤپAچ،‚ـ‚إپi‚ک,‚ƒ‚”پj‚ئ•\‹L‚µ‚ؤ‚¢‚½—v‘fˆت’u‚ًپAپi‚ƒ‚”,‚کپj‚ئ“ü‚ê‘ض‚¦‚ؤ‚¨‚«‚ـ‚·پB
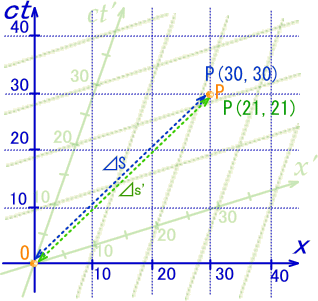
SŒn‚جچہ•WX ‚إ‚حP‚ج“ا‚ف‚حپi‚R‚OپC‚R‚Oپj‚إ‚·پBپ@‚و‚ء‚ؤ‹——£‚ً‡™S‚ئ‚·‚é‚ئ
پ@پ@پ@پ@
ˆê•ûپA—خ‚ج‚“پfŒnچہ•W‚ک‚إ‚جP‚ج“ا‚ف‚ح–ٌپi‚Q‚PپC‚Q‚PپjپA‚±‚ê‚حƒچپ[ƒŒƒ“ƒc•دٹ·
پ@پ@پ@پ@
‚ة‚و‚ء‚ؤ‹پ‚ك‚ç‚ê‚é’l‚إ‚à‚ ‚è‚ـ‚·پBپ@“¯—l‚ة‚“پfŒnچہ•W‚ک‚إ‚ج‹——£‚ًŒvژZ‚·‚é‚ئ
پ@پ@پ@پ@
ŒvژZ‚إٹm‚©‚ك‚é‚ـ‚إ‚à–³‚پA‚»‚ꂼ‚ê‚ج‹——£‚حˆظ‚ب‚è‚ـ‚·پBپ@‚±‚ê‚ح‚¢‚ء‚½‚¢‚ا‚¤‚¢‚¤ژ–‚إ‚µ‚ه‚¤پB
گو‚ظ‚اٹm‚©‚ك‚½پAƒAƒtƒ@ƒCƒ“•دٹ·‚ب‚ا‚جچہ•W•دٹ·‚إ‚حپA‹——£‚ح•s•د‚إ‚µ‚½پBپ@–œ‚ھˆêˆظ‚ب‚éڈêچ‡‚حپA•دٹ·ژ®‚ھŒë‚ء‚ؤ‚¢‚½ڈêچ‡‚إ‚µ‚©—L‚蓾‚ـ‚¹‚ٌپB
‚ئŒ¾‚¤ژ–‚حپAƒچپ[ƒŒƒ“ƒc•دٹ·‚ھٹشˆل‚ء‚ؤ‚¢‚é‚ج‚إ‚µ‚ه‚¤‚©پHپ@‚¢‚¦‚¢‚¦پA‚»‚جچl‚¦‚ح–{––“]“|‚إ‚·پBپ@ƒ~ƒ“ƒRƒtƒXƒLپ[ژ‹َ‚إ‚حچإڈ‰‚ةƒچپ[ƒŒƒ“ƒc•دٹ·‚ ‚è‚«‚إ‚·‚©‚çپB
‹^‚ي‚µ‚«‚ح‹——£‚ج’è‹`‚ئ‚ب‚è‚ـ‚·پBپ@‚ب‚؛‚ب‚çپAژٹش‚ئ‹َٹش‚ً–³—‚â‚èچ¬‚؛‚ؤ‚µ‚ـ‚ء‚½‚ج‚إ‚·‚©‚çپB
SŒn‚جچہ•WX‚ج“ا‚فپi‚R‚OپC‚R‚Oپj‚ئ‚“پfŒnچہ•W‚ک‚ج“ا‚فپi‚Q‚PپC‚Q‚Pپj‚ئ‚جٹش‚إ‹¤’ت‚ج—ت‚ح‰½‚ب‚ٌ‚إ‚µ‚ه‚¤‚©پH
‚؟‚ه‚ء‚ئچl‚¦‚é‚ئپ@‚R‚Oپ|‚R‚Oپپ‚OپAپ@‚Q‚Pپ|‚Q‚Pپپ‚Oپ@‚إˆّ‚«ژZ‚µ‚½’l‚ح‹¤’ت‚ج—ت‚إ‚·پB
ٹm‚©‚ةSŒn‚إ‚S‚Tپ‹‚جگüڈم‚حŒُ‚ج‹Oگص‚إ‚ ‚èپA‚“پfŒn‚àŒُ‘¬“x•s•د‚ة‚و‚èپA‚کپfپپ‚ƒ‚”پf‚ئ‚ب‚é‚و‚¤‚ةچہ•W‚ھŒX‚¢‚ؤ‚¢‚ـ‚·پBپ@‚ذ‚ه‚ئ‚µ‚½‚ç‹——£پFS‚حپ@‚ƒ‚”پ|Xپ@‚ب‚ج‚إ‚µ‚ه‚¤‚©پH
‚³‚ç‚ةچl‚¦‚é‚ئپAƒ†پ[ƒNƒٹƒbƒh‹َٹش‚إ‚ج‹——£S‚ح‚»‚ꂼ‚ê“ٌڈو‚µ‚ؤ‚ـ‚µ‚½پBپ@‚»‚ê‚ة‚ب‚ç‚ء‚ؤپA‚»‚ꂼ‚ê‚ً“ٌڈو‚µ‚½—ت‚ج‚X‚O‚Oپ|‚X‚O‚Oپپ‚OپA‚S‚S‚Pپ|‚S‚S‚Pپپ‚Oپ@‚ئ‚àچl‚¦‚ç‚ê‚ـ‚·پB
ˆب‰؛‚ج‚و‚¤‚ة•ت‚ج‚ج“_P‚إٹm”F‚µ‚ؤ‚ف‚ـ‚µ‚ه‚¤پB
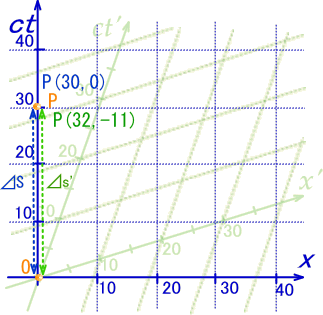
‚ا‚¤‚إ‚·‚©پHپ@‚R‚Oپ|‚Oپپ‚R‚OپAپ@‚R‚Qپ|‚P‚Pپپ‚Q‚P‚ئ‚ب‚è’Pڈƒ‚بˆّ‚«ژZ‚إ‚ح–³‚¢‚و‚¤‚إ‚·پBپ@‚à‚¤ˆê•û‚ج“ٌڈو‚·‚é•û‚جS‚إ‚حپ@‚X‚O‚Oپ|‚Oپپ‚X‚O‚OپAپ@‚P‚O‚Q‚Sپ|‚P‚Q‚Pپپ–ٌ‚X‚O‚Oپ@‚ئ‚ب‚ء‚ؤڈمژ肈ê’v‚µ‚ـ‚·پBپ@
”O‚ج‚½‚كپA‚à‚¤ˆêŒآڈٹٹm”F‚µ‚ؤ‚ف‚ـ‚µ‚ه‚¤پB
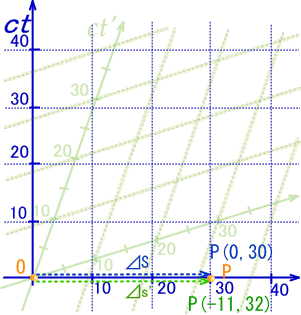
‚â‚ح‚è“ٌڈو‚·‚é•û‚جS‚إ‚حپ@‚Oپ|‚X‚O‚Oپپپ|‚X‚O‚OپAپ@‚P‚Q‚Pپ|‚P‚O‚Q‚Sپپ–ٌپ|‚X‚O‚Oپ@‚ئ‚ب‚ء‚ؤڈمژ肈ê’v‚µ‚ـ‚·پBپ@
‚±‚ج—l‚ة
‚±‚ج‹[ƒ†پ[ƒNƒٹƒbƒh‹َٹش‚جŒv—تپiƒپƒgƒٹƒbƒNƒeƒ“ƒ\ƒ‹پj‚حƒ~ƒ“ƒRƒtƒXƒLپ[Œv—ت‚ئŒؤ‚خ‚ê4Œ³•ھ‘S•”ڈ‘‚‚ئ
پ@پ@
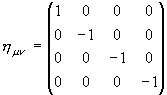
‚ئ‚ب‚è‚ـ‚·پB
‚SژںŒ³‚جچہ•Wژ²‚ً
پ@پ@
‚ئ•\Œ»‚·‚é‚ئپASŒn‚جچہ•WX‚ئ‚“پfŒnچہ•W‚ک‚ئ‚جٹضŒW‚ح
پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@
ƒچپ[ƒŒƒ“ƒc•دٹ·پAƒچپ[ƒŒƒ“ƒc‹t•دٹ·ژ®‚إ‚»‚ꂼ‚ê
پ@پ@
‚ئ•\‚³‚êپAژlژںŒ³‹——£پF‚„‚“‚ج“ٌڈو‚ح
پ@پ@
‚ئ‚ب‚èپA‚rŒnپA‚rپfŒn‹¤’ت•s•د‚ج—ت‚ئ‚ب‚è‚ـ‚·پB
پ@ˆب‰؛‚ةƒ†پ[ƒNƒٹƒbƒh‹َٹش‚ئ”نٹr‚µ‚ؤ‚ف‚ـ‚µ‚½
| چہ•W•دٹ·–¼ | ‹t•دٹ·ژ® | Œv—ت |
•دٹ·Œ³ |
ƒ~ƒ“ƒRƒtƒXƒLپ[ژ‹َ پi‹[ƒ†پ[ƒNƒٹƒbƒh‹َٹشپj پ@[ƒfƒJƒ‹ƒgچہ•W] |
پ@پ@ |
ƒچپ[ƒŒƒ“ƒcپi‹tپj•دٹ· |
پ@پ@ |
پ@‚à‚¤ˆê‚آ‚±‚جپw‹——£‚à‚ا‚«پx‚ئپw‹——£پx‚ئ‚جˆل‚¢‚إ‚·پB
“ٌ“_ٹش‚ج‚ًŒ‹‚شŒoکH‚جچإڈ¬’l‚ھ‹——£پiƒ†پ[ƒNƒٹƒbƒh‹َٹشپj‚إ‚ ‚é‚ج‚ة‘خ‚µپAچإ‘ه’l‚ھ‹——£پi‹[ƒ†پ[ƒNƒٹƒbƒh‹َٹشپj‚ئ‚ب‚é“_‚إ‚·پB
پ@ƒ†پ[ƒNƒٹƒbƒh‹َٹش‚إ‚جپw‹——£پx‚ح‰ٌ“]•دٹ·‚╽چsˆع“®•دٹ·‚ة‘خ‚µ‚ؤ•s•د—ت‚ئ‚ب‚ء‚ؤ‚¢‚ـ‚·پB‚»‚µ‚ؤƒ~ƒ“ƒRƒtƒXƒLپ[ژ‹َ‚إ‚جپw‹——£‚à‚ا‚«پx‚حƒچپ[ƒŒƒ“ƒc•دٹ·‚ة‘خ‚µ‚ؤ•s•د—ت‚ة‚ب‚ء‚ؤ‚¢‚ـ‚·پB