| 次の実験目的についてだが、今まで『曲がった空間』と言ってきたけれど、そもそも『曲がっている』ということはどういう事かを、はっきりと理解しておかなければならない。 これは、以前の実験で使った方眼紙。2次元空間が表せられる。つまりデカルト座標そのものだ。 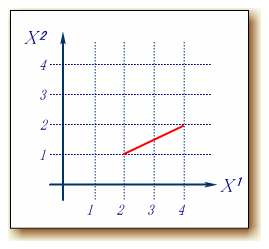 これを、ぐるっと筒状に丸めてみる。 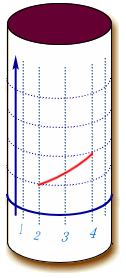 さあ、一見して、曲がった空間の出来上がり。 さて、これを曲がった空間に分類すべきか、だ。 方眼紙上の2次元空間とはいえ、これは4次元時空を2次元空間でモデル化しているものと思ってほしい。そういう意味では、この中で物理が完結する。 つまり、この座標を使って、物理の諸法則が定義される。 ところで、この曲がっているという事を認識できるのは、この2次元空間の外の、3次元空間から眺めている我々でしかない。この座標の中だけで定義される物理君が使える道具立ては2次元空間の計量でしかない。 例えば、貼りつける空間がユークリッド空間なら  であるし、ミンコフスキー時空なら  である。そしてこれを使って、物理法則が記述されることになる。 3次元空間の計量は、我々が使って意味の有るものであって、この筒の表面の物理君ごときがそれを共有できるものではない。 うん、ちょっと神様気分。 それでは、2次元空間の計量は、貼り付ける前と後ではどうなっているか？どうなっているもこうも無い。 丸める前の計量と同じだ。 つまり、物理空間は丸めても変わらない。 そういう訳で、この空間は『曲がった空間』に分類しないでおこう。 次は球面だ。 円筒形に習って、最初はボールに方眼紙を貼り付けようとしたのだが、端の方にいくほどしわが大きくなって全然貼っ付けられない。 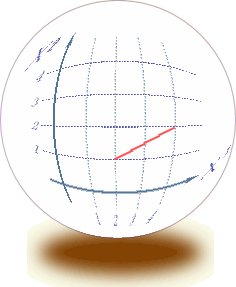 そこで、非常に柔らかいビニールシートに印刷し直して、それを無理やり貼り付けた。 ビニールシートはかなり伸びた部分が有って、もう少しで破れるところだった。 おかげで、座標の升目が伸びて変形してしまった。 これではデカルト座標の役目を果たさない。 やはり、球面は球面座標で表現するしかない。 そう、これではっきりした。球面はデカルト座標では表現できない。計量が異なっている。 そういうことで、球面は『曲がった空間』に分類しても良いだろう。 素直に見た目が曲がっているし。 ただ同じ様に、見た目が曲がっていた円筒の表面だが、意外なことにデカルト座標と同じ計量を持っていた。 そういう訳で、おしくも曲がった空間から外れてしまった。 球面の場合は、それと違って、ちゃんと計量が異なっている。 しかも、場所によって変形がひどくなっていた。 ただ、この  極座標でも場所が変わると計量が変化していた。 しかし極座標はいつでもデカルト座標に戻せるが、球面座標からは戻せない。 戻せないということは、この実験により明らかだ。 そこで、もっとこの曲がっているということを、直接的に表現する量がを考えてみよう。 そうそう、曲がっているという表現も今一だな。 日常会話では円筒形も曲がっていると言ってしまうし。 さっきの方眼紙を貼り付けた時の『しわの寄り具合』というのはどうだろうか？  曲がり具合の少ないと思われる大きなボールに方眼紙を貼り付ける場合は、しわの具合が少なかったから有力候補と言えるのでは。そもそも、しわって何で寄ってしまうのか？ 端の方に寄るほど、しわが多くなってしまう。 貼り付ける中心から遠ざかると、円周方向にだぶつきが出ているからだ。 中心から放射方向はだぶつききは無い。 結局、円周方向のだぶつきが原因となって、しわが現われる。 放射方向とは半径のことだ。 円周方向とは正に、円周長。 ユークリッド空間ではその比は円周率πで３.１４１５９２・・・と正確に決まっている。 半径に対し一方的に円周が短くなっていると言うことは、円周率が変わってしまっていると言うことだ。 そうすると空間の曲がり具合は、『しわしわ率』で定義できるように思われる。 『曲がり具合が大きい→しわしわ率が大きい→円周率が小さい』という関係だ。 円周率なら球面上にへばりついている"物理君"でも測定できる。 まずは、しわしわ率でどこまで曲がり具合が測れるかの実証実験だ。早速、球面物理世界に行って、実際に円周率の測定を行ってみよう。 よし、球面の物理世界に到着！  この球面に貼り付けたておいた物理空間は２次元リーマン空間だ。 別段、３次元空間でも、本物の4次元擬リーマン空間でも良かったんだが。 まあ、円周率の測定をしに来ただけだから、これで十分だろう。 どうやって立っているのかなんて、想像におまかせ。 4次元超球体に貼り付けた３次元空間を想像するよりは、まだましなんじゃないかな？ この球体の半径は1.90986Kｍ。 ただし、今はもう球面に貼り付けられた2次元物理空間の中にいるから、もはや元の球体を見るすべは無い。 どちらを向いても、真っ直ぐな水平線が見えるだけだ。 さて、持ってきた実験装置は、ロープと移動用のジープ1台。 ジープは走行距離メーター付きだから距離が測れる。 早速、円周率を測定しよう。 まず、この地点をO点として、ロープの端を固定。 ここから、真っ直ぐロープを引きながらジープで移動だ。 よし、１Km走行。 ちなみに事前の計算では、この距離は球面角度にして３０°地点だ。 ここをP点としてマーク。 OP間は１Km。 ロープの長さも１Kｍ。 これが半径となる。 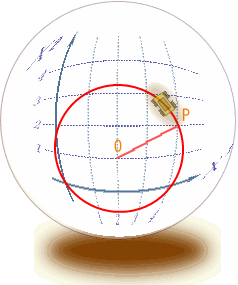 ここからロープをジープ側面に固定し、ロープをピンとはったまま、今度は円周方向に走行開始。 ぐるっと回って、先ほどのP地点に到着。 さて走行距離、つまり円周長は何Kmかな。 おう、丁度６Kｍぴったし！なかなか切りが良い数字だ。 さて、円周率の計算。 ６[ｋｍ]＝２πｒだから、ｒは１ｋｍだったので・・・、６割る２で３だ。円周率３．００００！ 実験成功。 自分自身が曲がっていることを、この2次元空間内の道具立てのみで見事確認できた。 ちなみに、この空間はしわが寄る空間だから『しわしわ率＋』の空間に分類しよう。 円筒表面空間でもやってみよう。 この空間は計量もデカルト座標そのものだったし、しわも寄らない。 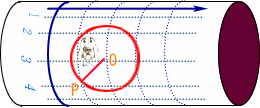 うん。何度やっても円周率は３.１41592・・・だ。『しわしわ率０』の空間といえる。 次は、これだ。鞍型の空間。 これは逆に円周が長くなるようだ。 しわが寄るというよりは、谷側では端が突っ張ってびりびりと裂けてしまう。 よし、これも円周率測定の実験だ。 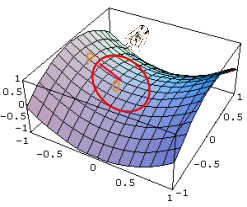 おー、やはり円周率はπより大きくなっている。 これは『しわしわ率−』の空間に分類するべきだ。 さて、今度の曲面は、出っ張っていて球面に似てるけど、球面ではない.。放物線の背中みたいだな。 しかも方向によって曲がり方が異なっている。 単純な球面と違うから、いろいろな場所で測ろう。 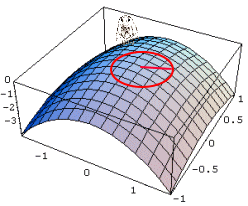 実験結果だが、 それぞれ球面と同じく円周率はπより小さかった。 お、測った場所によっては円周率は３．０も有る。 これでは最初に測った球面と区別が出来ない。 そうだな、このへんまでが『しわしわ率識別法』の限界かな。 単に円周率を測るだけじゃ球面の曲がり具合、つまり外から見た並の情報が失われている。 |
以上のメイの実験結果を、ガウスの曲面論におけるガウス曲率：Kを用いて整理してみましょう。 二次元曲面の外から見た曲がり具合の表現方法です。
まず、曲率を調べたい点を決めます。 その点近傍における曲面を2方向の曲線に分解し、方向別の曲線毎に半径ｒの接円を考えます。
各曲線の曲率K0、K1を（１/ｒ０）、（１/ｒ１）と定義します。なお、一方の円周が面の反対にある場合はｒをマイナスとします。 曲線の選び方は、曲率が最大と最小の二組とします。
これを使い
面の曲率：K=（K0×K1）
と、２つのパラメータで定義できます。 この曲率K=（+），（0），（-）がメイの言うところの『しわしわ率」、つまり円周率の大小に対応する量の様です。
『しわしわ率＋』の空間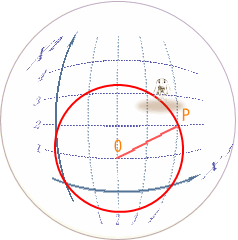 円周率＜π |
『しわしわ率0』の空間 円周率=π |
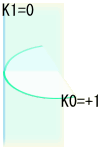
『しわしわ率−』の空間 円周率＞π |
  |
 |
 |
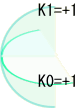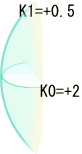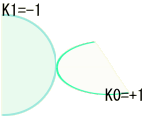| K=K0×K１=＋1 （正の曲率） |
K=K0×K１=0 （0の曲率） |
K=K0×K１=-１ （負の曲率） |
この様に、ガウス曲率：Kは曲面を大雑把に分類は出来るものの、形状までは表現できません。表現するためにはK0、K1という詳細なパラメーターが必要となります。しかしこのK0、K1はご覧の通り曲面の外、つまり、三次元空間より眺めて決められるパラメータです。
数学者のガウスは地球の測量に興味を持ち、円周率という内在的な量を用いて、曲面の曲り具合を定義できることに気付きました。 そして、それを基に、曲面論を考えたのです。
リーマン等の数学者は、さらにその曲面論を、非ユークリッド幾何学として発展させました。 非ユークリッド幾何学の一つであるリーマン幾何学で時空を表現し、一般相対性理論という形で重力理論を展開したのがアインシュタインです。 そして非ユークリッド幾何学にユークリッド幾何学が内包されたように、一般相対性理論（擬リーマン空間）に特殊相対性理論（ミンコフスキー時空）が内包され、相対性理論が完成したのです。
それでは、リーマン幾何学において、曲率はどのように扱われているのか調べて見ましょう。 メイの突撃実験も、どうやら壁に突き当たっている様ですし。