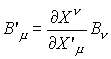その時空は4次元の距離を持った物理的実体です。器が4次元となった以上その中で記述される物理法則も4次元化する必要が有りそうです。そのためには物理量も4次元化しなければなりません。
物理量としては
無次元量 ： スカラー（Scalar)
次元依存量： 4元ベクトル(Vector)、4元テンソル(Tensor)
に分類されます。
スカラー量はそのままで、異なる時空（space-time)に共通な不変量となります。
ところが次元を持つベクトルやテンソルは不変量とはなりません。つまりローレンツ変換すると成分が変ってしまい、別物になってしまいます。
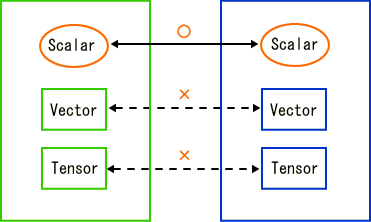
その具体例が物差しの長さであったりしました。
時計にとっては歯車が縮んだり、バネの強さが変わったり、はたまたテンプルの重さが変わったり。とてもまともに動きそうに思えない現象です。
それでも、それぞれの時空で、色々な物理的原理の異なる時計同士が、お互いに狂い無く動いていました。 共通にすべての時間が遅れていただけです。
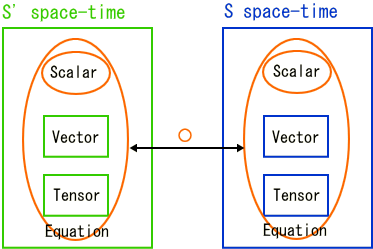
この事は、全ての物理的現象には4元量に基づく共通・不変の物理法則が有る。それにより原理の異なる時計にも関わらず、共通の動きが出来ていると言う事です。
例えば力学にも4元量を使って記述された、ローレンツ変換に不変な方程式（Ｅｑｕａｔｉｏｎ）が存在するはずです。
以下、それを探って見ましょう。
固有時間
先ほど、メイが質量を測る実験をしていた時使った重り時計
。 この時計はいつでも質点にくっついた、固有の時間を刻みます。これを固有時間：τと呼びます。何故、わざわざ固有時間と強調しているかというと、移動系の時間ｔ’は質点の速度に応じてその瞬間瞬間でテンポが変わってしまうからです。勿論速度が速いとゆっくりしたテンポになります。
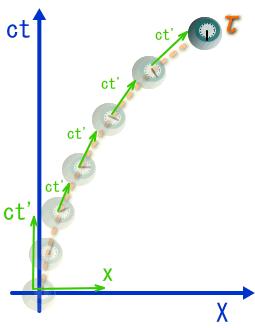
τは、質点が瞬間瞬間の速度に対応する移動系の時間ｔ’をつなぎ合わせたものと考えられます。
4元ベクトル
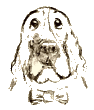 Dr.メイの『4元ベクトル理解のためのイメージトレーニング』！ （ミンコフスキー時空の復習） ベクトルの向きによりその大きさは変わる。一定では無い。つまり回転に対して不変ではない！勘違いの無いように。 位置ベクトルを例に。 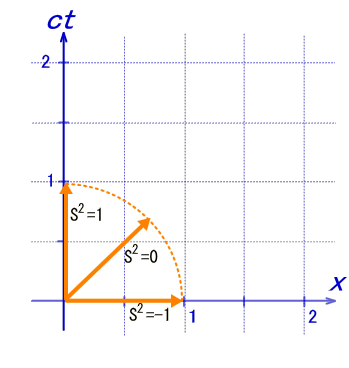 位置ベクトルの大きさ（=長さは）は時空距離に等しい。だから、向きにより、＋１のベクトル長が０、−１と変わってしまう。
この長さの定義では何に対して不変か？ それは勿論、 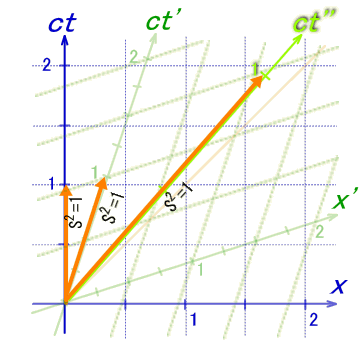 ごらんの通り、ローレンツ変換に対して不変！ まとめると、ユークリッド空間での長さは回転変換に不変。ミンコフスキー時空での長さはローレンツ変換に対して不変。  |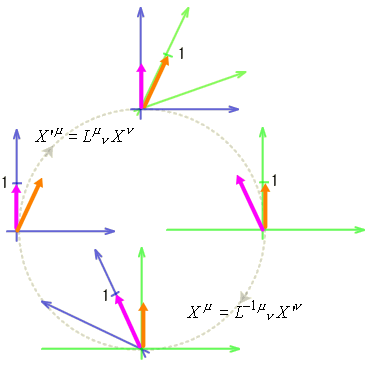
，
，
→ 
， 
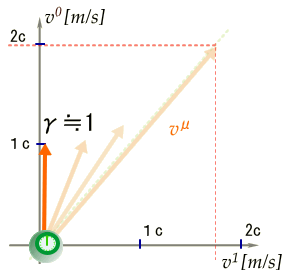
４元速度
この固有時間τを用いて、４元速度という新たな物理量
を定義してみましょう。以下、その４元速度の考察です。尚、質点を観測する立場・系において、空間成分（三次元分）はニュートン力学的な量と考えられ、３元××とか３次元××と呼び、特別に[V],[F]の様にカッコをつけて表現することにします。
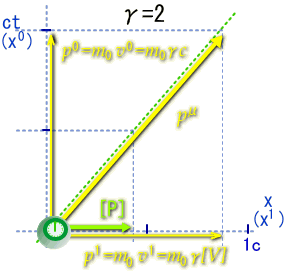
質点の３元速度[Ｖ]を約０．８７ｃとすると、γ係数は２となります。その場合の固有時間と静止系座標軸との関係は以下の通りです。
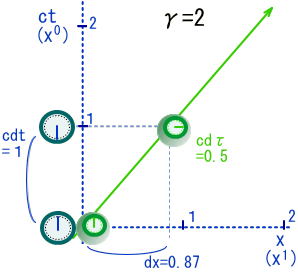
この図に対して４元速度：
のベクトルを重ねてみましょう。
より、空間成分：
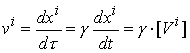
時間成分：
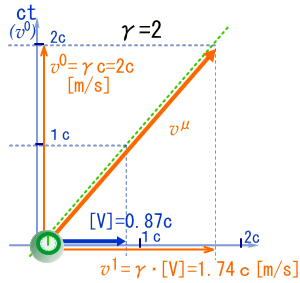
質点の３元速度が光速に比べて遅くなるにつれ、４元速度の空間成分ｖ1(=γ･V)は通常の速度、つまり３元速度：Vに近づきます。
また、時間成分はｖ0=γ･ｃにより光速度ｃに近づきます。 完全に静止している場合は時間成分ｃのみの４元ベクトルとなります。
固有時間：τはその瞬間の移動系の時間軸：ｔ’に等しので
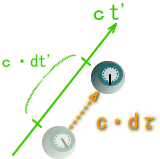
質点系では、
一方静止系では、τを使った４元速度
を用いると、
４次元距離の線素ｄｓは両系間で共通の不変量です。よって、
という恒等式が得られます。
４元加速度・４元力
この重り時計の質量をｍ0とし、Ｓ’系で[Ｆ]’の力で押した場合のニュートンの運動方程式は、この固有時間：τを使うと、
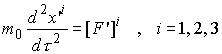
となります。
これを思い切って、4元化してみましょう。
但し、拡張した時間成分は
とします。この場合、左辺の２階微分項
は４元加速度、Ｆ’は4元力と言う事になります。この４元加速度と４元速度との関係を整理してみましょう。下の図は静止している重り時計にF’の力を加えた瞬間直後の状態です。
４元力ベクトルは無理やり速度座標に重ねていますので、単位が異なる異なる事に注意してください。
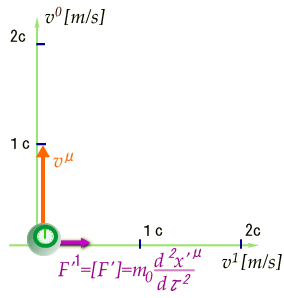
先ほどの
という条件の通り、４元加速度は空間成分のみ、また、速度ベクトルは静止状態では時間成分のみです。そして、それぞれのベクトルは直交しています。これは加速直後だけの現象の様に思えます。ところが前出の恒等式
をτで微分してみます。
↓
よって、
となり、４元速度ベクトルと４元加速度ベクトルは絶えず直交している事が分かります。
この様子を図に示しましょう。
まず、重り時計に力を掛けて加速していきます。そうすると速度が出てきて、質点の時空間座標が傾きはじめます。
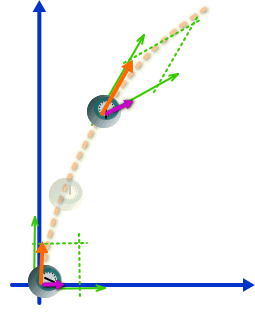
４元力ベクトルは空間座標の傾きに合わせて、閉じていきます。その結果速度ベクトルと４元加速度ベクトルは、このように光の軌跡を挟んで同じ角度で閉じあったベクトルになります。
この状況における４元力とニュートン力の関係を調べてみましょう。下の図はその詳細です。メモリの刻みは、取りあえず4元速度[m/S]方の単位で割り振っています。
＜＜＜＜＜以降要修正＞＞＞＞＞
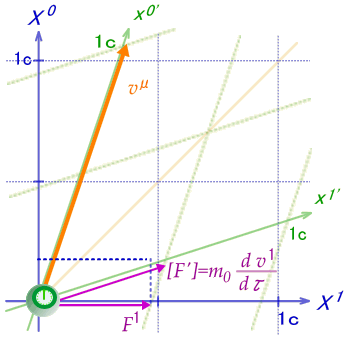
最初に、質点系で重り時計に働くニュートン力を考えます。これは空間成分のみですから、[F']とします。
これを静止系より見たニュートン力[F]とし４元力の空間成分をF1とします。この二つの３元力の関係を調べてみましょう。
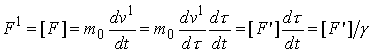
この関係はローレンツ収縮と同じです。
次に時間成分F0を求めてみましょう。直交関係の式
より、
両辺に質量をかけて
ここで
, 
であるから
よって、
つまり、空間成分と時間成分は下の図のように質点系空間軸の傾きに対応し、その結果、４元力ベクトルは空間軸に沿ったベクトルとなります。
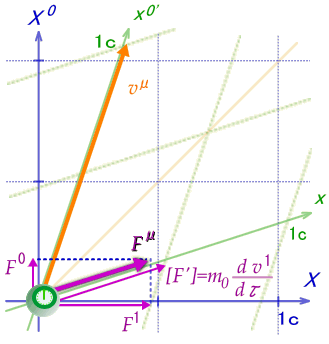
次に、４元運動方程式
はローレンツ不変であることを示しましょう。
まず、下の式はＳ系での運動方程式の左辺部分です。これを順次変形してみましょう。 尚、τはｄｓ2＝ｃ2ｄτ2であるためローレンツ不変です。
最初の変形は四次元位置ベクトルのxをローレンツ変換によりx'に変換しました。位置ベクトルですからローレンツ変換の対象そのものです。
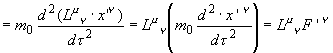
以降、係数でしかないＬを微分項より括り出し、カッコ内をＦ’に置き換えました。
結局、
と変形できました。
ところで元々のＳ'系での4元力の定義は、左辺の位置ベクトルｘの２階微分で、右辺が４元力Ｆでした。等式で有る以上、左辺と同様に変換されるべきです。つまり
と書けるはずです。よって、
となり、Ｓ系、Ｓ’系共に同じ方程式を得る事が出来ました。
Ｓ 系：
Ｓ'系：
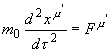
つまり、ニュートン力学の基礎方程式を４元化し、ローレンツ不変な方程式とする事に成功した訳です。
さて、ここまでで４元加速度と４元力が登場しました。次は４元運動量に関する考察です。
４元運動量
この調子で行くと、４元運動量は
となります。
先ほどの４元速度と同じ様に、時間軸成分と空間軸成分に分解してみましょう。
３元運動量：
とすると、
相対論的な質量
を用いると、４元運動量の空間成分と時間成分はそれぞれ、
, 
と書く事が出来ます。
また、空間成分において３元運度量Pを用いると、４元運動量ｐは
となります。
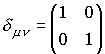
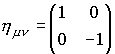
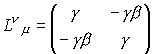
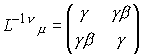
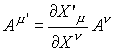